Question Number 82071 by jagoll last updated on 18/Feb/20
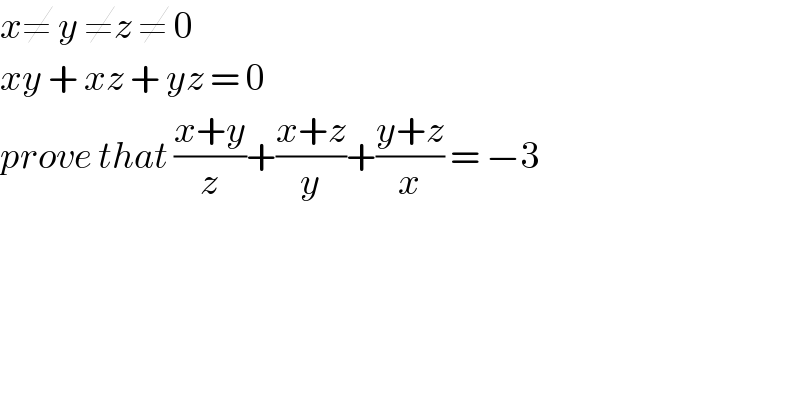
$${x}\neq\:{y}\:\neq{z}\:\neq\:\mathrm{0} \\ $$$${xy}\:+\:{xz}\:+\:{yz}\:=\:\mathrm{0} \\ $$$${prove}\:{that}\:\frac{{x}+{y}}{{z}}+\frac{{x}+{z}}{{y}}+\frac{{y}+{z}}{{x}}\:=\:−\mathrm{3} \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 18/Feb/20
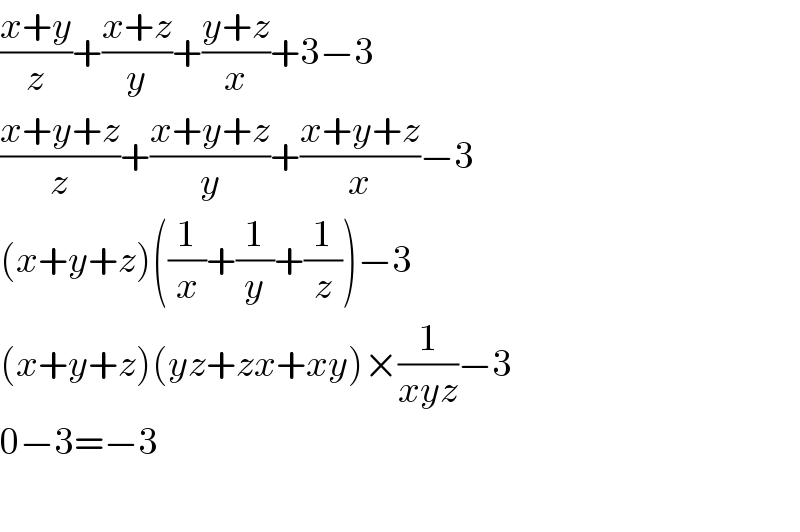
$$\frac{{x}+{y}}{{z}}+\frac{{x}+{z}}{{y}}+\frac{{y}+{z}}{{x}}+\mathrm{3}−\mathrm{3} \\ $$$$\frac{{x}+{y}+{z}}{{z}}+\frac{{x}+{y}+{z}}{{y}}+\frac{{x}+{y}+{z}}{{x}}−\mathrm{3} \\ $$$$\left({x}+{y}+{z}\right)\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)−\mathrm{3} \\ $$$$\left({x}+{y}+{z}\right)\left({yz}+{zx}+{xy}\right)×\frac{\mathrm{1}}{{xyz}}−\mathrm{3} \\ $$$$\mathrm{0}−\mathrm{3}=−\mathrm{3} \\ $$$$ \\ $$
Commented by jagoll last updated on 18/Feb/20

$${thank}\:{you}\:{sir} \\ $$
Answered by MJS last updated on 18/Feb/20

$${xy}+{xz}+{yz}=\mathrm{0}\:\Rightarrow\:{z}=−\frac{{xy}}{{x}+{y}} \\ $$$$\frac{{x}+{y}}{−\frac{{xy}}{{x}+{y}}}+\frac{{x}−\frac{{xy}}{{x}+{y}}}{{y}}+\frac{{y}−\frac{{xy}}{{x}+{y}}}{{x}}= \\ $$$$=−\frac{\left({x}+{y}\right)^{\mathrm{2}} }{{xy}}+\frac{{x}^{\mathrm{2}} }{\left({x}+{y}\right){y}}+\frac{{y}^{\mathrm{2}} }{{x}\left({x}+{y}\right)}= \\ $$$$=\frac{−\left({x}+{y}\right)^{\mathrm{3}} +{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }{{x}\left({x}+{y}\right){y}}=\frac{−\mathrm{3}{x}^{\mathrm{2}} {y}−\mathrm{3}{xy}^{\mathrm{2}} }{{x}\left({x}+{y}\right){y}}= \\ $$$$=\frac{−\mathrm{3}{x}\left({x}+{y}\right){y}}{{x}\left({x}+{y}\right){y}}=−\mathrm{3} \\ $$
Commented by jagoll last updated on 18/Feb/20

$${thank}\:{you}\:{mister} \\ $$
