Menu Close

x-y-z-4-z-t-x-3-y-z-t-4-t-x-y-1-find-the-value-of-x-2-y-2-z-2-t-2-

Tinku Tara 0 Comments
Pin




Question Number 90225 by jagoll last updated on 22/Apr/20
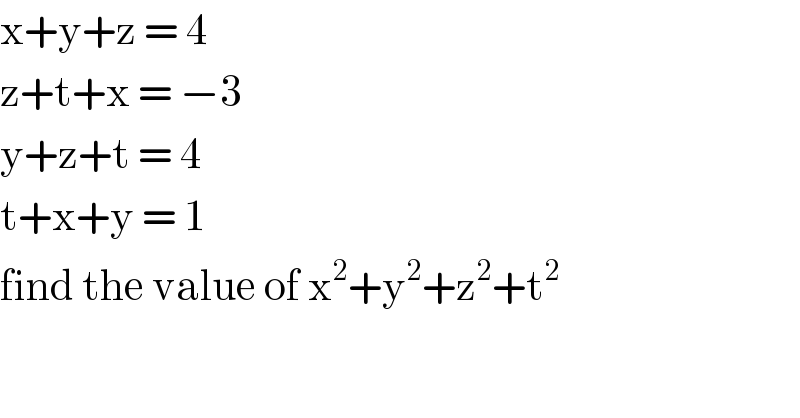
x+y+z = 4 z+t+x = −3 y+z+t = 4 t+x+y = 1 find the value of x^2 +y^2 +z^2 +t^2
$$\mathrm{x}+\mathrm{y}+\mathrm{z}\:=\:\mathrm{4} \\ $$$$\mathrm{z}+\mathrm{t}+\mathrm{x}\:=\:−\mathrm{3} \\ $$$$\mathrm{y}+\mathrm{z}+\mathrm{t}\:=\:\mathrm{4} \\ $$$$\mathrm{t}+\mathrm{x}+\mathrm{y}\:=\:\mathrm{1} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \: \\ $$
Commented by niroj last updated on 22/Apr/20
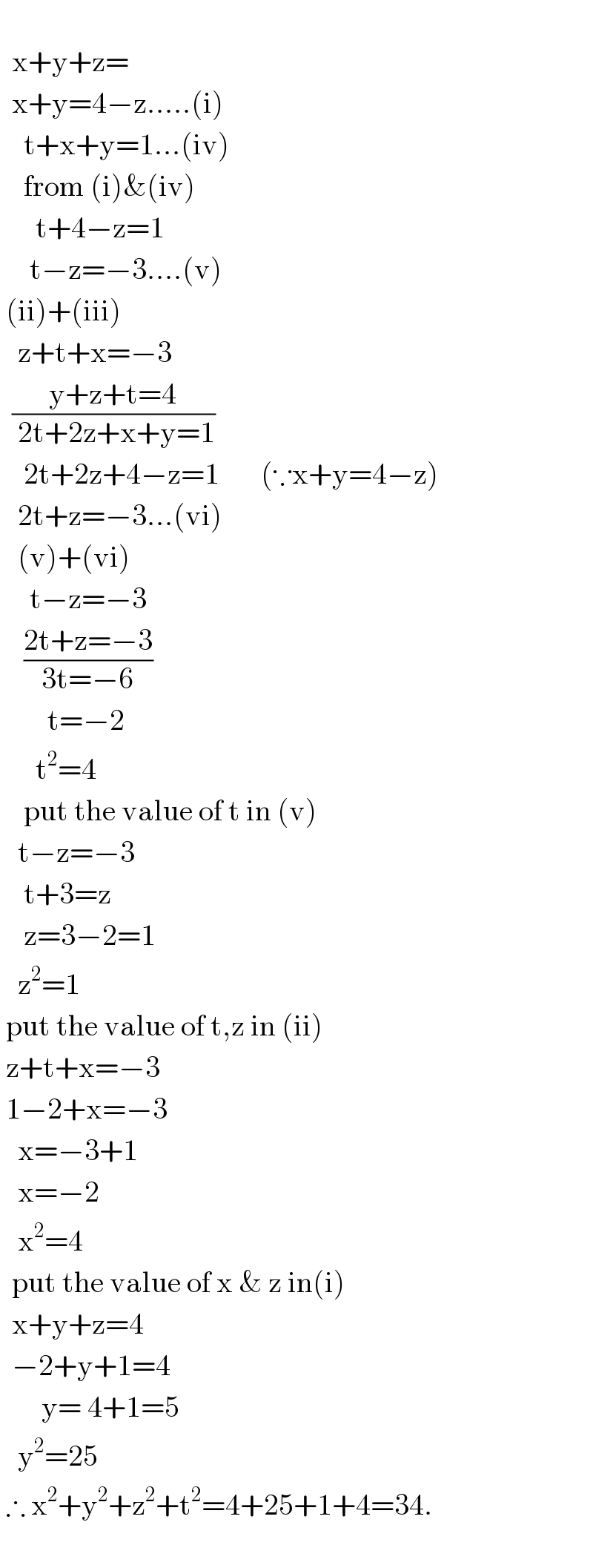
x+y+z= x+y=4−z.....(i) t+x+y=1...(iv) from (i)&(iv) t+4−z=1 t−z=−3....(v) (ii)+(iii) z+t+x=−3 ((y+z+t=4)/( 2t+2z+x+y=1)) 2t+2z+4−z=1 (∵x+y=4−z) 2t+z=−3...(vi) (v)+(vi) t−z=−3 ((2t+z=−3)/(3t=−6)) t=−2 t^2 =4 put the value of t in (v) t−z=−3 t+3=z z=3−2=1 z^2 =1 put the value of t,z in (ii) z+t+x=−3 1−2+x=−3 x=−3+1 x=−2 x^2 =4 put the value of x & z in(i) x+y+z=4 −2+y+1=4 y= 4+1=5 y^2 =25 ∴ x^2 +y^2 +z^2 +t^2 =4+25+1+4=34.
$$\:\: \\ $$$$\:\:\mathrm{x}+\mathrm{y}+\mathrm{z}= \\ $$$$\:\:\mathrm{x}+\mathrm{y}=\mathrm{4}−\mathrm{z}…..\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\mathrm{t}+\mathrm{x}+\mathrm{y}=\mathrm{1}…\left(\mathrm{iv}\right) \\ $$$$\:\:\:\:\mathrm{from}\:\left(\mathrm{i}\right)\&\left(\mathrm{iv}\right) \\ $$$$\:\:\:\:\:\:\mathrm{t}+\mathrm{4}−\mathrm{z}=\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{t}−\mathrm{z}=−\mathrm{3}….\left(\mathrm{v}\right) \\ $$$$\:\left(\mathrm{ii}\right)+\left(\mathrm{iii}\right) \\ $$$$\:\:\:\mathrm{z}+\mathrm{t}+\mathrm{x}=−\mathrm{3} \\ $$$$\:\:\frac{\mathrm{y}+\mathrm{z}+\mathrm{t}=\mathrm{4}}{\:\mathrm{2t}+\mathrm{2z}+\mathrm{x}+\mathrm{y}=\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{2t}+\mathrm{2z}+\mathrm{4}−\mathrm{z}=\mathrm{1}\:\:\:\:\:\:\:\left(\because\mathrm{x}+\mathrm{y}=\mathrm{4}−\mathrm{z}\right) \\ $$$$\:\:\:\mathrm{2t}+\mathrm{z}=−\mathrm{3}…\left(\mathrm{vi}\right) \\ $$$$\:\:\:\left(\mathrm{v}\right)+\left(\mathrm{vi}\right) \\ $$$$\:\:\:\:\:\mathrm{t}−\mathrm{z}=−\mathrm{3} \\ $$$$\:\:\:\:\frac{\mathrm{2t}+\mathrm{z}=−\mathrm{3}}{\mathrm{3t}=−\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{t}=−\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{t}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\mathrm{put}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{t}\:\mathrm{in}\:\left(\mathrm{v}\right) \\ $$$$\:\:\:\mathrm{t}−\mathrm{z}=−\mathrm{3} \\ $$$$\:\:\:\:\mathrm{t}+\mathrm{3}=\mathrm{z} \\ $$$$\:\:\:\:\mathrm{z}=\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$$\:\:\:\mathrm{z}^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\mathrm{put}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{t},\mathrm{z}\:\mathrm{in}\:\left(\mathrm{ii}\right) \\ $$$$\:\mathrm{z}+\mathrm{t}+\mathrm{x}=−\mathrm{3} \\ $$$$\:\mathrm{1}−\mathrm{2}+\mathrm{x}=−\mathrm{3} \\ $$$$\:\:\:\mathrm{x}=−\mathrm{3}+\mathrm{1} \\ $$$$\:\:\:\mathrm{x}=−\mathrm{2} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\mathrm{put}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\&\:\mathrm{z}\:\mathrm{in}\left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{4} \\ $$$$\:\:−\mathrm{2}+\mathrm{y}+\mathrm{1}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{y}=\:\mathrm{4}+\mathrm{1}=\mathrm{5} \\ $$$$\:\:\:\mathrm{y}^{\mathrm{2}} =\mathrm{25} \\ $$$$\:\therefore\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} =\mathrm{4}+\mathrm{25}+\mathrm{1}+\mathrm{4}=\mathrm{34}. \\ $$$$\:\:\:\: \\ $$
Commented by Prithwish Sen 1 last updated on 22/Apr/20
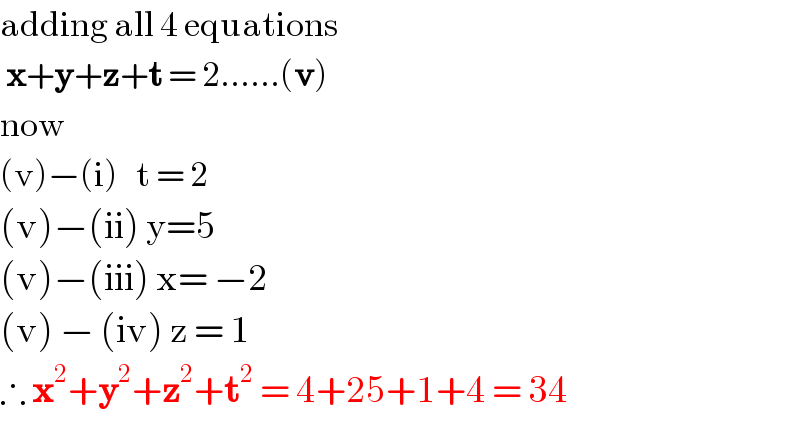
adding all 4 equations x+y+z+t = 2......(v) now (v)−(i) t = 2 (v)−(ii) y=5 (v)−(iii) x= −2 (v) − (iv) z = 1 ∴ x^2 +y^2 +z^2 +t^2 = 4+25+1+4 = 34
$$\mathrm{adding}\:\mathrm{all}\:\mathrm{4}\:\mathrm{equations} \\ $$$$\:\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{t}}\:=\:\mathrm{2}……\left(\boldsymbol{\mathrm{v}}\right) \\ $$$$\mathrm{now} \\ $$$$\left(\mathrm{v}\right)−\left(\mathrm{i}\right)\:\:\:\mathrm{t}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{v}\right)−\left(\mathrm{ii}\right)\:\mathrm{y}=\mathrm{5} \\ $$$$\left(\mathrm{v}\right)−\left(\mathrm{iii}\right)\:\mathrm{x}=\:−\mathrm{2} \\ $$$$\left(\mathrm{v}\right)\:−\:\left(\mathrm{iv}\right)\:\mathrm{z}\:=\:\mathrm{1} \\ $$$$\therefore\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\boldsymbol{\mathrm{t}}^{\mathrm{2}} \:=\:\mathrm{4}+\mathrm{25}+\mathrm{1}+\mathrm{4}\:=\:\mathrm{34} \\ $$
Commented by jagoll last updated on 22/Apr/20
thank you all
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *