Question Number 120952 by abony1303 last updated on 04/Nov/20

$$\mathrm{x},\mathrm{y},\mathrm{z}\:{are}\:{real}\:{numbers} \\ $$$$\begin{cases}{\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{4}}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{10}}\\{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +\mathrm{z}^{\mathrm{3}} =\mathrm{22}}\end{cases}\:\:\:\:\:{Find}\:\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} +\mathrm{z}^{\mathrm{4}} \\ $$
Answered by MJS_new last updated on 04/Nov/20
![z=4−x−y let x=u−(√v)∧y=u+(√v) ⇒ { ((z=4−2u)),((2v+2(3u^2 −8u+3)=0)),((6uv−6(u^3 −8u^2 +16u−7)=0)) :} ⇒ −3u^2 −8u+3=((u^3 −8u^2 +16u−7)/u) ⇔ u^3 −4u^2 +((19)/4)u−(7/4)=0 ⇔ (u−1)(u−((3−(√2))/2))(u−((3+(√2))/2))=0 take u=1 [or any other of the solutions] ⇒ v=2 ⇒ x=1−(√2)∧y=1+(√2)∧z=2 ⇒ answer is 50](https://www.tinkutara.com/question/Q120968.png)
$${z}=\mathrm{4}−{x}−{y} \\ $$$$\mathrm{let}\:{x}={u}−\sqrt{{v}}\wedge{y}={u}+\sqrt{{v}} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{z}=\mathrm{4}−\mathrm{2}{u}}\\{\mathrm{2}{v}+\mathrm{2}\left(\mathrm{3}{u}^{\mathrm{2}} −\mathrm{8}{u}+\mathrm{3}\right)=\mathrm{0}}\\{\mathrm{6}{uv}−\mathrm{6}\left({u}^{\mathrm{3}} −\mathrm{8}{u}^{\mathrm{2}} +\mathrm{16}{u}−\mathrm{7}\right)=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\:−\mathrm{3}{u}^{\mathrm{2}} −\mathrm{8}{u}+\mathrm{3}=\frac{{u}^{\mathrm{3}} −\mathrm{8}{u}^{\mathrm{2}} +\mathrm{16}{u}−\mathrm{7}}{{u}} \\ $$$$\Leftrightarrow\:{u}^{\mathrm{3}} −\mathrm{4}{u}^{\mathrm{2}} +\frac{\mathrm{19}}{\mathrm{4}}{u}−\frac{\mathrm{7}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Leftrightarrow\:\left({u}−\mathrm{1}\right)\left({u}−\frac{\mathrm{3}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\left({u}−\frac{\mathrm{3}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{take}\:{u}=\mathrm{1}\:\left[\mathrm{or}\:\mathrm{any}\:\mathrm{other}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solutions}\right] \\ $$$$\Rightarrow\:{v}=\mathrm{2} \\ $$$$\Rightarrow\:{x}=\mathrm{1}−\sqrt{\mathrm{2}}\wedge{y}=\mathrm{1}+\sqrt{\mathrm{2}}\wedge{z}=\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{50} \\ $$
Answered by Jamshidbek2311 last updated on 04/Nov/20
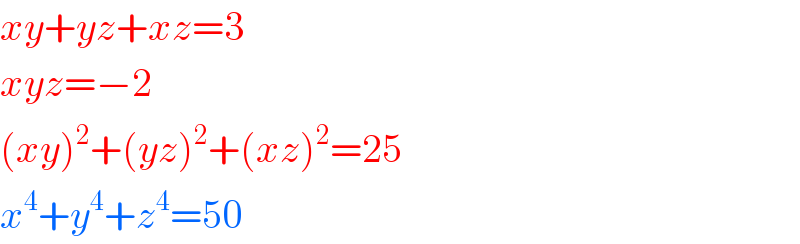
$${xy}+{yz}+{xz}=\mathrm{3} \\ $$$${xyz}=−\mathrm{2} \\ $$$$\left({xy}\right)^{\mathrm{2}} +\left({yz}\right)^{\mathrm{2}} +\left({xz}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{50} \\ $$
