Question Number 161242 by HongKing last updated on 14/Dec/21
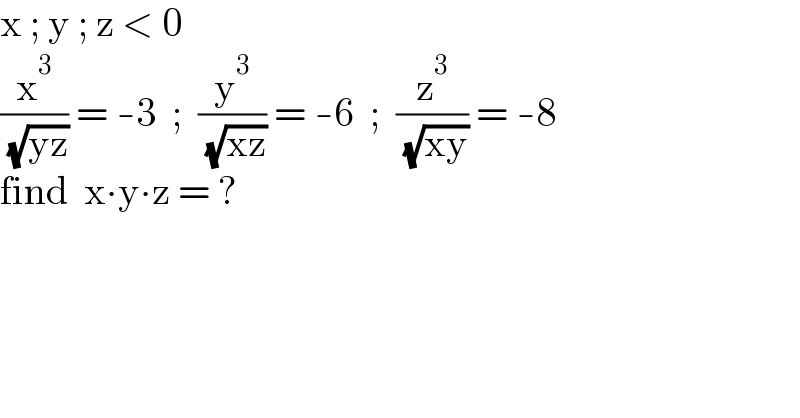
$$\mathrm{x}\:;\:\mathrm{y}\:;\:\mathrm{z}\:<\:\mathrm{0} \\ $$$$\frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{yz}}}\:=\:-\mathrm{3}\:\:;\:\:\frac{\mathrm{y}^{\mathrm{3}} }{\:\sqrt{\mathrm{xz}}}\:=\:-\mathrm{6}\:\:;\:\:\frac{\mathrm{z}^{\mathrm{3}} }{\:\sqrt{\mathrm{xy}}}\:=\:-\mathrm{8} \\ $$$$\mathrm{find}\:\:\mathrm{x}\centerdot\mathrm{y}\centerdot\mathrm{z}\:=\:? \\ $$
Answered by mr W last updated on 15/Dec/21
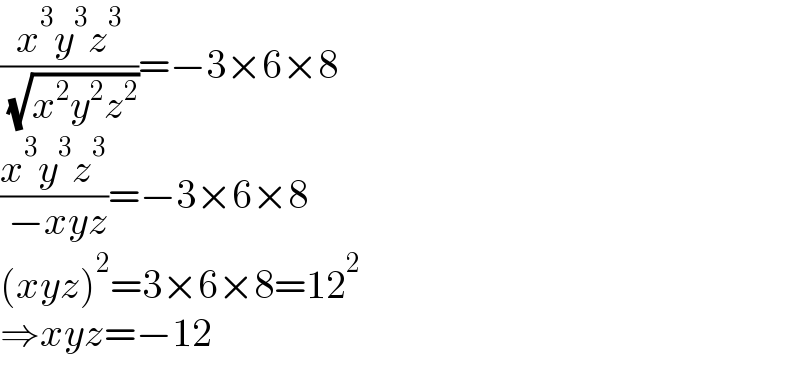
$$\frac{{x}^{\mathrm{3}} {y}^{\mathrm{3}} {z}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} }}=−\mathrm{3}×\mathrm{6}×\mathrm{8} \\ $$$$\frac{{x}^{\mathrm{3}} {y}^{\mathrm{3}} {z}^{\mathrm{3}} }{\:−{xyz}}=−\mathrm{3}×\mathrm{6}×\mathrm{8} \\ $$$$\left({xyz}\right)^{\mathrm{2}} =\mathrm{3}×\mathrm{6}×\mathrm{8}=\mathrm{12}^{\mathrm{2}} \\ $$$$\Rightarrow{xyz}=−\mathrm{12} \\ $$
Commented by HongKing last updated on 17/Dec/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{cool} \\ $$
