Menu Close

x-y-z-R-If-1-x-1-y-z-1-2-1-y-1-x-z-1-3-1-z-1-x-y-1-4-x-y-z-

Tinku Tara 0 Comments
Pin




Question Number 183668 by mnjuly1970 last updated on 28/Dec/22
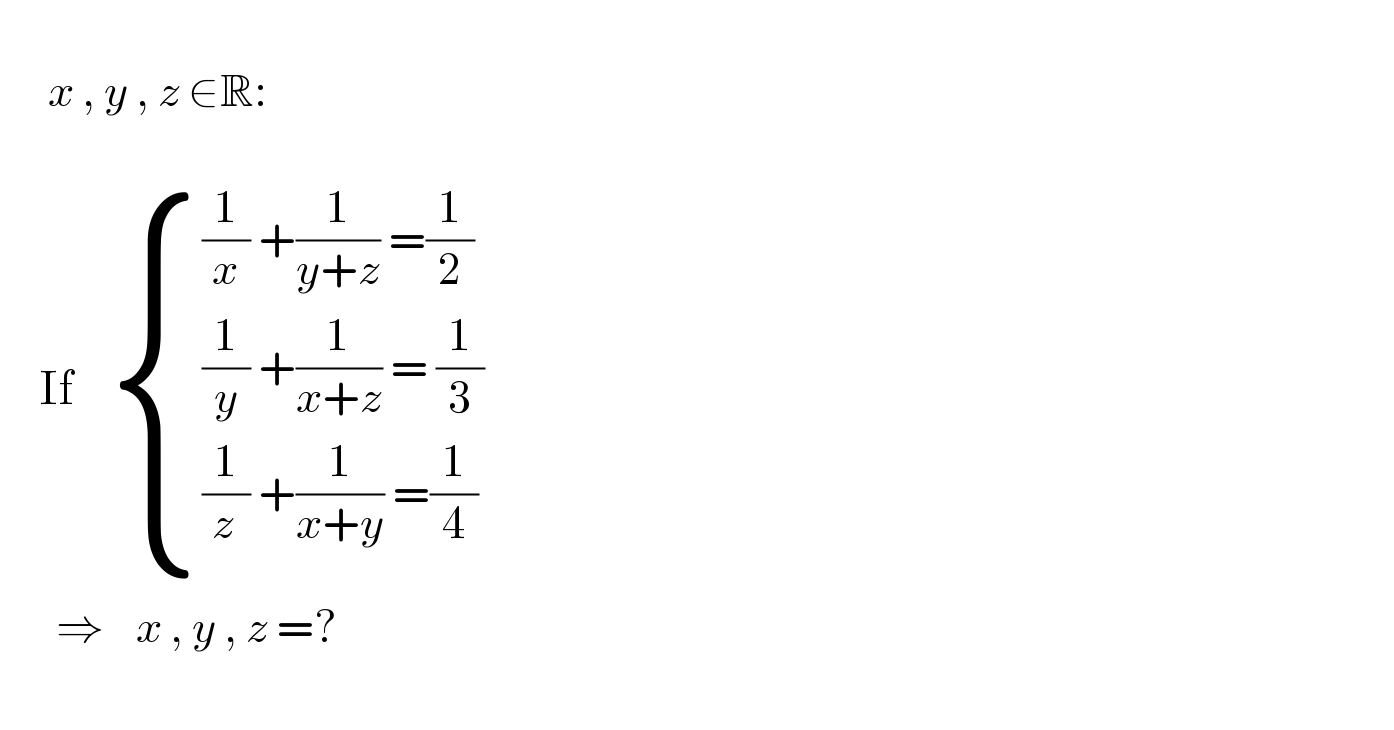
x , y , z ∈R: If { (((1/x) +(1/(y+z)) =(1/2))),(((1/y) +(1/(x+z)) = (1/3))),(((1/z_ ) +(1/(x+y)) =(1/4))) :} ⇒ x , y , z =?
$$ \\ $$$$\:\:\:\:\:\:{x}\:,\:{y}\:,\:{z}\:\in\mathbb{R}: \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\mathrm{If}\:\:\:\:\begin{cases}{\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{y}+{z}}\:=\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{{y}}\:+\frac{\mathrm{1}}{{x}+{z}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{{z}_{\:} }\:+\frac{\mathrm{1}}{{x}+{y}}\:=\frac{\mathrm{1}}{\mathrm{4}}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\:\:\:{x}\:,\:{y}\:,\:{z}\:=? \\ $$$$ \\ $$
Commented by Frix last updated on 28/Dec/22
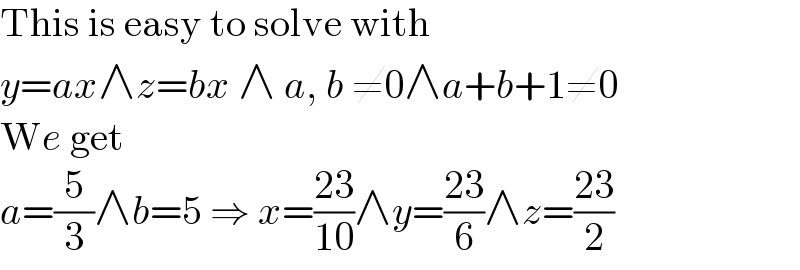
This is easy to solve with y=ax∧z=bx ∧ a, b ≠0∧a+b+1≠0 We get a=(5/3)∧b=5 ⇒ x=((23)/(10))∧y=((23)/6)∧z=((23)/2)
$$\mathrm{This}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{with} \\ $$$${y}={ax}\wedge{z}={bx}\:\wedge\:{a},\:{b}\:\neq\mathrm{0}\wedge{a}+{b}+\mathrm{1}\neq\mathrm{0} \\ $$$$\mathrm{W}{e}\:\mathrm{get} \\ $$$${a}=\frac{\mathrm{5}}{\mathrm{3}}\wedge{b}=\mathrm{5}\:\Rightarrow\:{x}=\frac{\mathrm{23}}{\mathrm{10}}\wedge{y}=\frac{\mathrm{23}}{\mathrm{6}}\wedge{z}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Dec/22
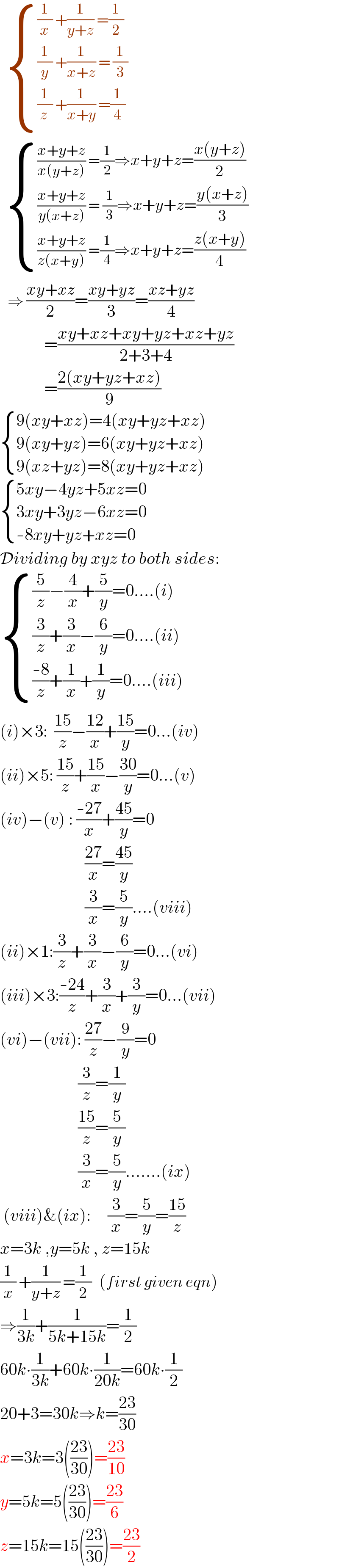
{ (((1/x) +(1/(y+z)) =(1/2))),(((1/y) +(1/(x+z)) = (1/3))),(((1/z_ ) +(1/(x+y)) =(1/4))) :} { ((((x+y+z)/(x(y+z))) =(1/2)⇒x+y+z=((x(y+z))/2))),((((x+y+z)/(y(x+z))) = (1/3)⇒x+y+z=((y(x+z))/3))),((((x+y+z)/(z(x+y))) =(1/4)⇒x+y+z=((z(x+y))/4))) :} ⇒ ((xy+xz)/2)=((xy+yz)/3)=((xz+yz)/4) =((xy+xz+xy+yz+xz+yz)/(2+3+4)) =((2(xy+yz+xz))/9) { ((9(xy+xz)=4(xy+yz+xz))),((9(xy+yz)=6(xy+yz+xz))),((9(xz+yz)=8(xy+yz+xz))) :} { ((5xy−4yz+5xz=0)),((3xy+3yz−6xz=0)),((-8xy+yz+xz=0)) :} Dividing by xyz to both sides: { (((5/z)−(4/x)+(5/y)=0....(i))),(((3/z)+(3/x)−(6/y)=0....(ii))),((((-8)/z)+(1/x)+(1/y)=0....(iii))) :} (i)×3: ((15)/z)−((12)/x)+((15)/y)=0...(iv) (ii)×5: ((15)/z)+((15)/x)−((30)/y)=0...(v) (iv)−(v) : ((-27)/x)+((45)/y)=0 ((27)/x)=((45)/y) (3/x)=(5/y)....(viii) (ii)×1:(3/z)+(3/x)−(6/y)=0...(vi) (iii)×3:((-24)/z)+(3/x)+(3/y)=0...(vii) (vi)−(vii): ((27)/z)−(9/y)=0 (3/z)=(1/y) ((15)/z)=(5/y) (3/x)=(5/y).......(ix) (viii)&(ix): (3/x)=(5/y)=((15)/z) x=3k ,y=5k , z=15k (1/x) +(1/(y+z)) =(1/2) (first given eqn) ⇒(1/(3k))+(1/(5k+15k))=(1/2) 60k∙(1/(3k))+60k∙(1/(20k))=60k∙(1/2) 20+3=30k⇒k=((23)/(30)) x=3k=3(((23)/(30)))=((23)/(10)) y=5k=5(((23)/(30)))=((23)/6) z=15k=15(((23)/(30)))=((23)/2)
$$\:\:\begin{cases}{\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{y}+{z}}\:=\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{{y}}\:+\frac{\mathrm{1}}{{x}+{z}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{{z}_{\:} }\:+\frac{\mathrm{1}}{{x}+{y}}\:=\frac{\mathrm{1}}{\mathrm{4}}}\end{cases}\:\:\: \\ $$$$\:\:\begin{cases}{\frac{{x}+{y}+{z}}{{x}\left({y}+{z}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}+{y}+{z}=\frac{{x}\left({y}+{z}\right)}{\mathrm{2}}}\\{\frac{{x}+{y}+{z}}{{y}\left({x}+{z}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{x}+{y}+{z}=\frac{{y}\left({x}+{z}\right)}{\mathrm{3}}}\\{\frac{{x}+{y}+{z}}{{z}\left({x}+{y}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{x}+{y}+{z}=\frac{{z}\left({x}+{y}\right)}{\mathrm{4}}}\end{cases}\:\:\: \\ $$$$\:\:\:\Rightarrow\:\frac{{xy}+{xz}}{\mathrm{2}}=\frac{{xy}+{yz}}{\mathrm{3}}=\frac{{xz}+{yz}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{xy}+{xz}+{xy}+{yz}+{xz}+{yz}}{\mathrm{2}+\mathrm{3}+\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\left({xy}+{yz}+{xz}\right)}{\mathrm{9}} \\ $$$$\begin{cases}{\mathrm{9}\left({xy}+{xz}\right)=\mathrm{4}\left({xy}+{yz}+{xz}\right)}\\{\mathrm{9}\left({xy}+{yz}\right)=\mathrm{6}\left({xy}+{yz}+{xz}\right)}\\{\mathrm{9}\left({xz}+{yz}\right)=\mathrm{8}\left({xy}+{yz}+{xz}\right)}\end{cases} \\ $$$$\begin{cases}{\mathrm{5}{xy}−\mathrm{4}{yz}+\mathrm{5}{xz}=\mathrm{0}}\\{\mathrm{3}{xy}+\mathrm{3}{yz}−\mathrm{6}{xz}=\mathrm{0}}\\{-\mathrm{8}{xy}+{yz}+{xz}=\mathrm{0}}\end{cases} \\ $$$$\mathcal{D}{ividing}\:{by}\:{xyz}\:{to}\:{both}\:{sides}: \\ $$$$\begin{cases}{\frac{\mathrm{5}}{{z}}−\frac{\mathrm{4}}{{x}}+\frac{\mathrm{5}}{{y}}=\mathrm{0}….\left({i}\right)}\\{\frac{\mathrm{3}}{{z}}+\frac{\mathrm{3}}{{x}}−\frac{\mathrm{6}}{{y}}=\mathrm{0}….\left({ii}\right)}\\{\frac{-\mathrm{8}}{{z}}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\mathrm{0}….\left({iii}\right)}\end{cases} \\ $$$$\left({i}\right)×\mathrm{3}:\:\:\frac{\mathrm{15}}{{z}}−\frac{\mathrm{12}}{{x}}+\frac{\mathrm{15}}{{y}}=\mathrm{0}…\left({iv}\right) \\ $$$$\left({ii}\right)×\mathrm{5}:\:\frac{\mathrm{15}}{{z}}+\frac{\mathrm{15}}{{x}}−\frac{\mathrm{30}}{{y}}=\mathrm{0}…\left({v}\right) \\ $$$$\left({iv}\right)−\left({v}\right)\::\:\frac{-\mathrm{27}}{{x}}+\frac{\mathrm{45}}{{y}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{27}}{{x}}=\frac{\mathrm{45}}{{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{{x}}=\frac{\mathrm{5}}{{y}}….\left({viii}\right) \\ $$$$\left({ii}\right)×\mathrm{1}:\frac{\mathrm{3}}{{z}}+\frac{\mathrm{3}}{{x}}−\frac{\mathrm{6}}{{y}}=\mathrm{0}…\left({vi}\right) \\ $$$$\left({iii}\right)×\mathrm{3}:\frac{-\mathrm{24}}{{z}}+\frac{\mathrm{3}}{{x}}+\frac{\mathrm{3}}{{y}}=\mathrm{0}…\left({vii}\right) \\ $$$$\left({vi}\right)−\left({vii}\right):\:\frac{\mathrm{27}}{{z}}−\frac{\mathrm{9}}{{y}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{{z}}=\frac{\mathrm{1}}{{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{15}}{{z}}=\frac{\mathrm{5}}{{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{{x}}=\frac{\mathrm{5}}{{y}}…….\left({ix}\right) \\ $$$$\:\left({viii}\right)\&\left({ix}\right):\:\:\:\:\:\frac{\mathrm{3}}{{x}}=\frac{\mathrm{5}}{{y}}=\frac{\mathrm{15}}{{z}} \\ $$$${x}=\mathrm{3}{k}\:,{y}=\mathrm{5}{k}\:,\:{z}=\mathrm{15}{k} \\ $$$$\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{y}+{z}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\left({first}\:{given}\:{eqn}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{3}{k}}+\frac{\mathrm{1}}{\mathrm{5}{k}+\mathrm{15}{k}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{60}{k}\centerdot\frac{\mathrm{1}}{\mathrm{3}{k}}+\mathrm{60}{k}\centerdot\frac{\mathrm{1}}{\mathrm{20}{k}}=\mathrm{60}{k}\centerdot\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{20}+\mathrm{3}=\mathrm{30}{k}\Rightarrow{k}=\frac{\mathrm{23}}{\mathrm{30}} \\ $$$${x}=\mathrm{3}{k}=\mathrm{3}\left(\frac{\mathrm{23}}{\mathrm{30}}\right)=\frac{\mathrm{23}}{\mathrm{10}} \\ $$$${y}=\mathrm{5}{k}=\mathrm{5}\left(\frac{\mathrm{23}}{\mathrm{30}}\right)=\frac{\mathrm{23}}{\mathrm{6}} \\ $$$${z}=\mathrm{15}{k}=\mathrm{15}\left(\frac{\mathrm{23}}{\mathrm{30}}\right)=\frac{\mathrm{23}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 29/Dec/22
tanks alot ali ...
$${tanks}\:{alot}\:{ali}\:… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *