Question Number 99513 by naka3546 last updated on 21/Jun/20
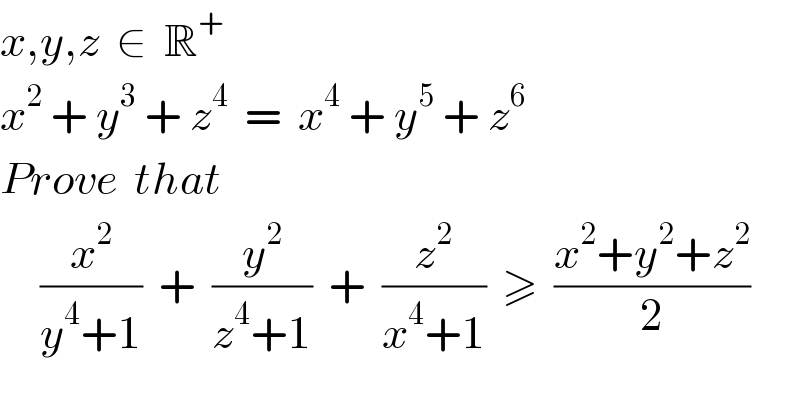
$${x},{y},{z}\:\:\in\:\:\mathbb{R}^{+} \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{4}} \:\:=\:\:{x}^{\mathrm{4}} \:+\:{y}^{\mathrm{5}} \:+\:{z}^{\mathrm{6}} \\ $$$${Prove}\:\:{that} \\ $$$$\:\:\:\:\:\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{4}} +\mathrm{1}}\:\:+\:\:\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{4}} +\mathrm{1}}\:\:+\:\:\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{1}}\:\:\geqslant\:\:\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jun/20
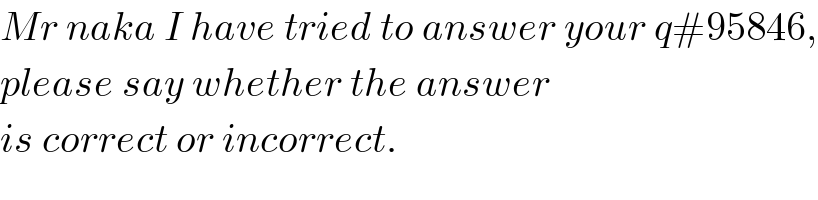
$${Mr}\:{naka}\:{I}\:{have}\:{tried}\:{to}\:{answer}\:{your}\:{q}#\mathrm{95846}, \\ $$$${please}\:{say}\:{whether}\:{the}\:{answer} \\ $$$${is}\:{correct}\:{or}\:{incorrect}. \\ $$
Commented by naka3546 last updated on 22/Jun/20
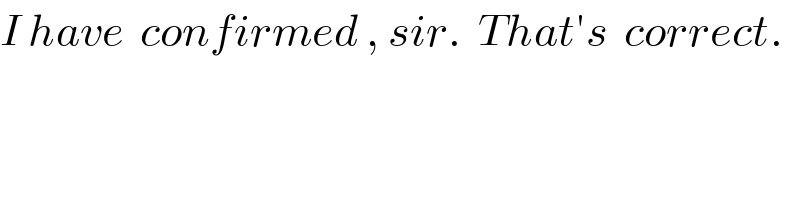
$${I}\:{have}\:\:{confirmed}\:,\:{sir}.\:\:{That}'{s}\:\:{correct}. \\ $$
