Question Number 125743 by MathSh last updated on 13/Dec/20
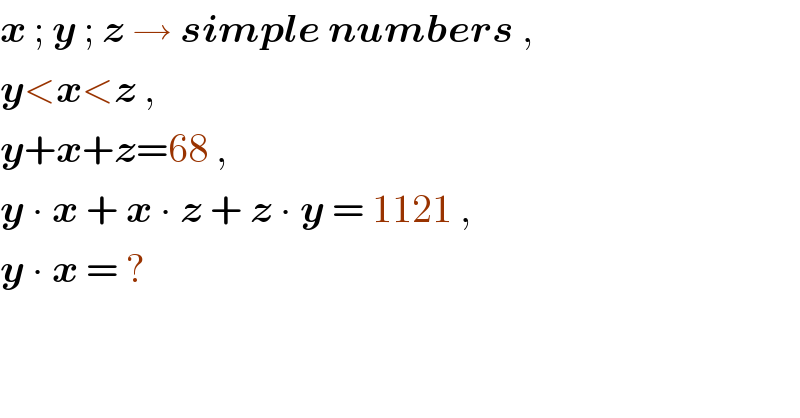
$$\boldsymbol{{x}}\:;\:\boldsymbol{{y}}\:;\:\boldsymbol{{z}}\:\rightarrow\:\boldsymbol{{simple}}\:\boldsymbol{{numbers}}\:, \\ $$$$\boldsymbol{{y}}<\boldsymbol{{x}}<\boldsymbol{{z}}\:, \\ $$$$\boldsymbol{{y}}+\boldsymbol{{x}}+\boldsymbol{{z}}=\mathrm{68}\:, \\ $$$$\boldsymbol{{y}}\:\centerdot\:\boldsymbol{{x}}\:+\:\boldsymbol{{x}}\:\centerdot\:\boldsymbol{{z}}\:+\:\boldsymbol{{z}}\:\centerdot\:\boldsymbol{{y}}\:=\:\mathrm{1121}\:, \\ $$$$\boldsymbol{{y}}\:\centerdot\:\boldsymbol{{x}}\:=\:? \\ $$
Commented by MJS_new last updated on 13/Dec/20
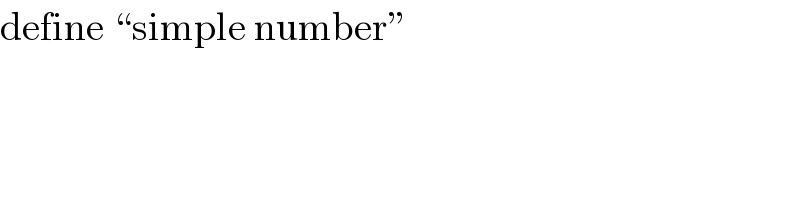
$$\mathrm{define}\:“\mathrm{simple}\:\mathrm{number}'' \\ $$
Commented by MathSh last updated on 13/Dec/20
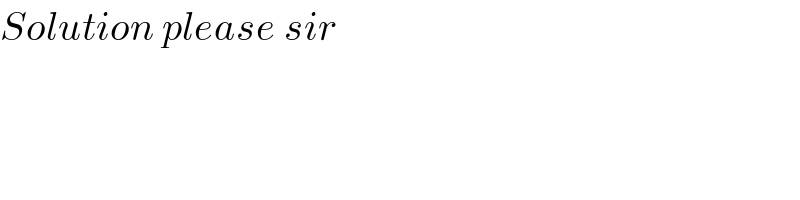
$${Solution}\:{please}\:{sir} \\ $$
Commented by MJS_new last updated on 13/Dec/20
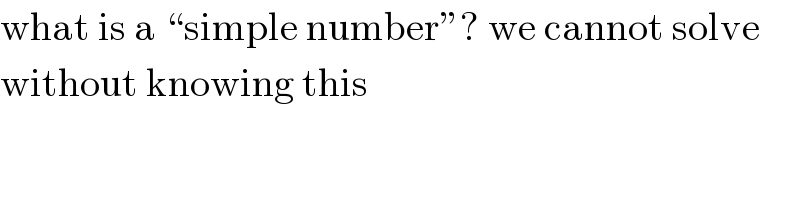
$$\mathrm{what}\:\mathrm{is}\:\mathrm{a}\:“\mathrm{simple}\:\mathrm{number}''?\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{solve} \\ $$$$\mathrm{without}\:\mathrm{knowing}\:\mathrm{this} \\ $$
Commented by MathSh last updated on 13/Dec/20
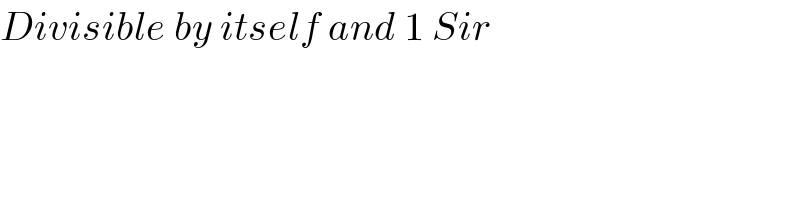
$${Divisible}\:{by}\:{itself}\:{and}\:\mathrm{1}\:{Sir} \\ $$
Commented by Her_Majesty last updated on 13/Dec/20
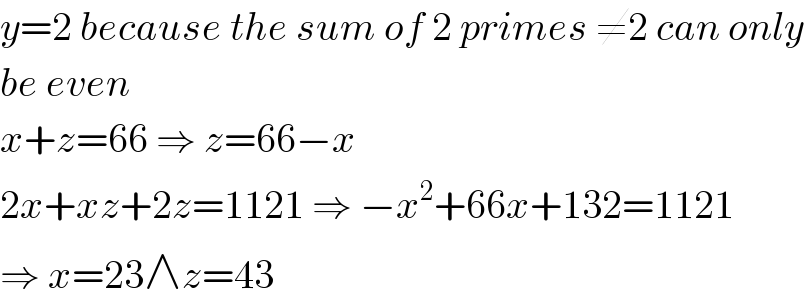
$${y}=\mathrm{2}\:{because}\:{the}\:{sum}\:{of}\:\mathrm{2}\:{primes}\:\neq\mathrm{2}\:{can}\:{only} \\ $$$${be}\:{even} \\ $$$${x}+{z}=\mathrm{66}\:\Rightarrow\:{z}=\mathrm{66}−{x} \\ $$$$\mathrm{2}{x}+{xz}+\mathrm{2}{z}=\mathrm{1121}\:\Rightarrow\:−{x}^{\mathrm{2}} +\mathrm{66}{x}+\mathrm{132}=\mathrm{1121} \\ $$$$\Rightarrow\:{x}=\mathrm{23}\wedge{z}=\mathrm{43} \\ $$
Commented by MJS_new last updated on 13/Dec/20

$$\mathrm{ok}\:\mathrm{I}\:\mathrm{was}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{you}\:\mathrm{mean}\:{primes}\:\mathrm{or}\:\mathrm{maybe} \\ $$$${whole}\:{numbers}. \\ $$$$\mathrm{if}\:{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{prime}\:\mathrm{numbers}\:\mathrm{then}\:\mathrm{I}\:\mathrm{guess}\:\mathrm{they} \\ $$$$\mathrm{are}\:>\mathrm{0}.\:\mathrm{then}\:\mathrm{if}\:\mathrm{their}\:\mathrm{sum}\:\mathrm{is}\:\mathrm{even}\:\Rightarrow\:\mathrm{one}\:\mathrm{of} \\ $$$$\mathrm{them}\:\mathrm{must}\:\mathrm{equal}\:\mathrm{2}.\:{y}<{x}<{z}\:\Rightarrow\:{y}=\mathrm{2} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}+{x}+{z}=\mathrm{68}\:\Leftrightarrow\:{x}+{z}=\mathrm{66} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}{x}+{xz}+\mathrm{2}{z}=\mathrm{1121} \\ $$$$ \\ $$$$\mathrm{2}\left({x}+{z}\right)+{xz}=\mathrm{1121} \\ $$$${xz}=\mathrm{989}=\mathrm{23}×\mathrm{43} \\ $$$$\Rightarrow\:{x}=\mathrm{23}\:{y}=\mathrm{2}\:{z}=\mathrm{43} \\ $$$$\Rightarrow\:{xy}=\mathrm{46} \\ $$
Commented by MathSh last updated on 13/Dec/20
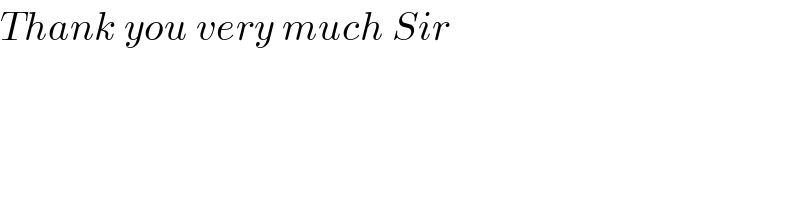
$${Thank}\:{you}\:{very}\:{much}\:{Sir} \\ $$
