Question Number 158303 by HongKing last updated on 02/Nov/21
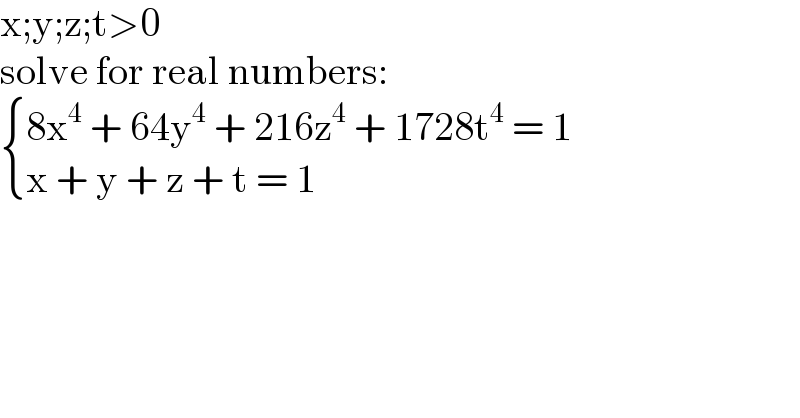
$$\mathrm{x};\mathrm{y};\mathrm{z};\mathrm{t}>\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\begin{cases}{\mathrm{8x}^{\mathrm{4}} \:+\:\mathrm{64y}^{\mathrm{4}} \:+\:\mathrm{216z}^{\mathrm{4}} \:+\:\mathrm{1728t}^{\mathrm{4}} \:=\:\mathrm{1}}\\{\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:+\:\mathrm{t}\:=\:\mathrm{1}}\end{cases} \\ $$$$ \\ $$
Answered by mr W last updated on 02/Nov/21
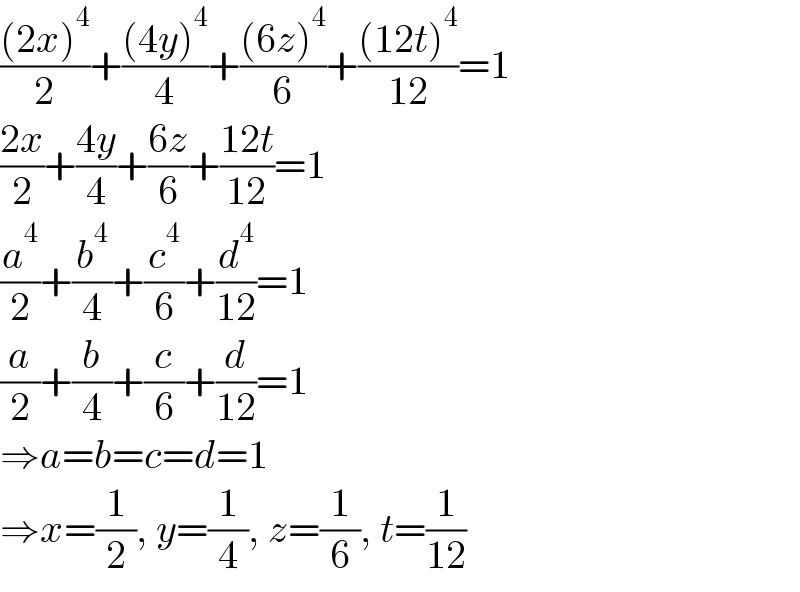
$$\frac{\left(\mathrm{2}{x}\right)^{\mathrm{4}} }{\mathrm{2}}+\frac{\left(\mathrm{4}{y}\right)^{\mathrm{4}} }{\mathrm{4}}+\frac{\left(\mathrm{6}{z}\right)^{\mathrm{4}} }{\mathrm{6}}+\frac{\left(\mathrm{12}{t}\right)^{\mathrm{4}} }{\mathrm{12}}=\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{\mathrm{2}}+\frac{\mathrm{4}{y}}{\mathrm{4}}+\frac{\mathrm{6}{z}}{\mathrm{6}}+\frac{\mathrm{12}{t}}{\mathrm{12}}=\mathrm{1} \\ $$$$\frac{{a}^{\mathrm{4}} }{\mathrm{2}}+\frac{{b}^{\mathrm{4}} }{\mathrm{4}}+\frac{{c}^{\mathrm{4}} }{\mathrm{6}}+\frac{{d}^{\mathrm{4}} }{\mathrm{12}}=\mathrm{1} \\ $$$$\frac{{a}}{\mathrm{2}}+\frac{{b}}{\mathrm{4}}+\frac{{c}}{\mathrm{6}}+\frac{{d}}{\mathrm{12}}=\mathrm{1} \\ $$$$\Rightarrow{a}={b}={c}={d}=\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}},\:{y}=\frac{\mathrm{1}}{\mathrm{4}},\:{z}=\frac{\mathrm{1}}{\mathrm{6}},\:{t}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Commented by HongKing last updated on 02/Nov/21
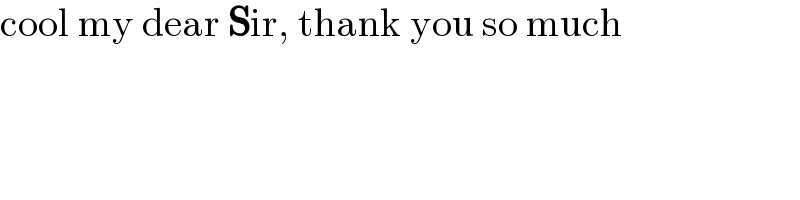
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{ir},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
