Question Number 117116 by mathocean1 last updated on 10/Oct/20
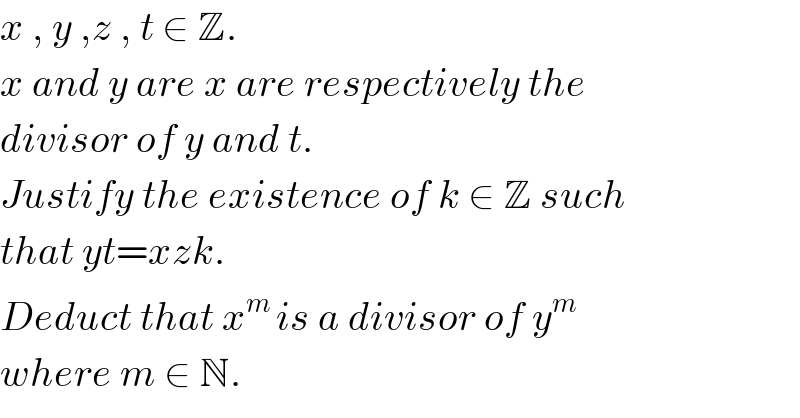
$${x}\:,\:{y}\:,{z}\:,\:{t}\:\in\:\mathbb{Z}. \\ $$$${x}\:{and}\:{y}\:{are}\:{x}\:{are}\:{respectively}\:{the} \\ $$$${divisor}\:{of}\:{y}\:{and}\:{t}. \\ $$$${Justify}\:{the}\:{existence}\:{of}\:{k}\:\in\:\mathbb{Z}\:{such} \\ $$$${that}\:{yt}={xzk}. \\ $$$${Deduct}\:{that}\:{x}^{{m}\:} {is}\:{a}\:{divisor}\:{of}\:{y}^{{m}} \\ $$$${where}\:{m}\:\in\:\mathbb{N}. \\ $$
Commented by 1549442205PVT last updated on 10/Oct/20

$$\mathrm{In}\:\mathrm{R}\:\mathrm{there}\:\mathrm{is}\:\:\mathrm{no}\:\:\mathrm{concept}\:\mathrm{of}\:\:\mathrm{a}\:\:\mathrm{divisor} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{number}.\mathrm{It}\:\mathrm{only}\:\mathrm{is}\:\mathrm{said}\:\mathrm{in}\:\mathrm{Z}.\mathrm{You} \\ $$$$\mathrm{look}\:\mathrm{at}\:\mathrm{question}\:\mathrm{again},\mathrm{please}. \\ $$
Commented by mathocean1 last updated on 10/Oct/20

$${exactly}\:{it}\:{was}\:{an}\:{error} \\ $$
