Question Number 59381 by Karan last updated on 09/May/19

$$\:\:\int\frac{{xdx}}{\mathrm{sin}\:{x}}\:=\:? \\ $$
Commented by Mr X pcx last updated on 11/May/19
![let g(x) =∫_0 ^x (t/(sint))dt we have t−(t^3 /6) ≤sint ≤t for all t∈[0,x] and x>0 (1/t) ≤ (1/(sint)) ≤(1/(t−(t^3 /6))) ⇒1 ≤ (t/(sint)) ≤ (1/(1−(t^2 /6))) ⇒x ≤ ∫_0 ^x (t/(sint)) dt ≤ ∫_0 ^x (dt/(1−(t^2 /6))) but ∫_0 ^x (dt/(1−(t^2 /6))) =_(t=(√6)u) ∫_0 ^(x/( (√6))) (((√6)du)/(1−u^2 )) =((√6)/2) ∫_0 ^(x/( (√6))) ((1/(1+u)) +(1/(1−u)))du =((√6)/2)[ln∣((1+u)/(1−u))∣]_0 ^(x/( (√6))) =((√6)/2)ln∣((1+(x/( (√6))))/(1−(x/( (√6)))))∣ =((√6)/2)ln∣(((√6)+x)/( (√6)−x))∣ ⇒ x≤ ∫_0 ^x (t/(sint))dt ≤ ((√6)/2)ln∣(((√6)+x)/( (√6)−x))∣ (x≥0) .](https://www.tinkutara.com/question/Q59521.png)
$${let}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}}{{sint}}{dt}\:{we}\:{have}\: \\ $$$${t}−\frac{{t}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant{sint}\:\leqslant{t}\:\:\:\:{for}\:{all}\:{t}\in\left[\mathrm{0},{x}\right]\:{and}\:{x}>\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{t}}\:\leqslant\:\frac{\mathrm{1}}{{sint}}\:\leqslant\frac{\mathrm{1}}{{t}−\frac{{t}^{\mathrm{3}} }{\mathrm{6}}}\:\Rightarrow\mathrm{1}\:\leqslant\:\frac{{t}}{{sint}}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{6}}} \\ $$$$\Rightarrow{x}\:\leqslant\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}}{{sint}}\:{dt}\:\leqslant\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{dt}}{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{6}}}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{dt}}{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{6}}}\:=_{{t}=\sqrt{\mathrm{6}}{u}} \:\:\:\:\int_{\mathrm{0}} ^{\frac{{x}}{\:\sqrt{\mathrm{6}}}} \:\:\:\:\:\:\frac{\sqrt{\mathrm{6}}{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{{x}}{\:\sqrt{\mathrm{6}}}} \:\:\left(\frac{\mathrm{1}}{\mathrm{1}+{u}}\:+\frac{\mathrm{1}}{\mathrm{1}−{u}}\right){du} \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\frac{{x}}{\:\sqrt{\mathrm{6}}}} \:\:\:=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+\frac{{x}}{\:\sqrt{\mathrm{6}}}}{\mathrm{1}−\frac{{x}}{\:\sqrt{\mathrm{6}}}}\mid \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\mathrm{6}}+{x}}{\:\sqrt{\mathrm{6}}−{x}}\mid\:\Rightarrow \\ $$$${x}\leqslant\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}}{{sint}}{dt}\:\leqslant\:\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\mathrm{6}}+{x}}{\:\sqrt{\mathrm{6}}−{x}}\mid\:\:\left({x}\geqslant\mathrm{0}\right)\:. \\ $$
Commented by Mr X pcx last updated on 11/May/19
![no elementsry function but let take this try we can return to the form f(x) =∫_0 ^x (t/(sint)) dt chang.tan((t/2))=u give f(x)=∫_0 ^(tan((x/2))) ((2arctanu)/((2u)/(1+u^2 ))) ((2du)/(1+u^2 )) =2 ∫_0 ^(tan((x/2))) ((arctan(u))/u) du let w(α) =∫_0 ^(tan((x/2))) ((arctan(αu))/u) du ⇒ w^′ (α) =∫_0 ^(tan((x/2))) (du/(1+α^2 u^2 )) =_(αu=y) ∫_0 ^(αtan((x/2))) (dy/(α(1+y^2 ))) =(1/α) [arctan(y)]_0 ^(αtan((x/2))) =(1/α) arctan(αtan((x/2))) ⇒ w(α)=∫_0 ^α (1/t) arctan(ttan((x/2)))dt +c c=w(0)=0 ⇒w(α)=∫_0 ^α (1/t) arctan(ttan((x/2)))dt f(x)=2w(1) =2 ∫_0 ^1 (1/t) arctan(tan((x/2))t)dt ....be continued....](https://www.tinkutara.com/question/Q59520.png)
$${no}\:{elementsry}\:{function}\:{but}\:{let}\:{take} \\ $$$${this}\:{try}\:{we}\:{can}\:{return}\:{to}\:{the}\:{form} \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}}{{sint}}\:{dt}\:\:{chang}.{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u} \\ $$$${give}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\frac{\mathrm{2}{arctanu}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\:\:\frac{{arctan}\left({u}\right)}{{u}}\:{du} \\ $$$${let}\:{w}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{{arctan}\left(\alpha{u}\right)}{{u}}\:{du}\:\Rightarrow \\ $$$${w}^{'} \left(\alpha\right)\:=\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\:\frac{{du}}{\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$$=_{\alpha{u}={y}} \:\:\:\:\:\int_{\mathrm{0}} ^{\alpha{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\:\:\frac{{dy}}{\alpha\left(\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\alpha}\:\left[{arctan}\left({y}\right)\right]_{\mathrm{0}} ^{\alpha{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\alpha}\:{arctan}\left(\alpha{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$${w}\left(\alpha\right)=\int_{\mathrm{0}} ^{\alpha} \:\:\:\frac{\mathrm{1}}{{t}}\:{arctan}\left({ttan}\left(\frac{{x}}{\mathrm{2}}\right)\right){dt}\:+{c} \\ $$$${c}={w}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{w}\left(\alpha\right)=\int_{\mathrm{0}} ^{\alpha} \:\:\frac{\mathrm{1}}{{t}}\:{arctan}\left({ttan}\left(\frac{{x}}{\mathrm{2}}\right)\right){dt} \\ $$$${f}\left({x}\right)=\mathrm{2}{w}\left(\mathrm{1}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{t}}\:{arctan}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right){t}\right){dt} \\ $$$$….{be}\:{continued}…. \\ $$
Commented by Mr X pcx last updated on 11/May/19
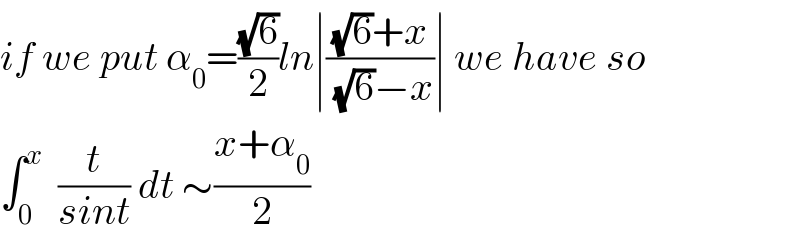
$${if}\:{we}\:{put}\:\alpha_{\mathrm{0}} =\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\mathrm{6}}+{x}}{\:\sqrt{\mathrm{6}}−{x}}\mid\:{we}\:{have}\:{so} \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}}{{sint}}\:{dt}\:\sim\frac{{x}+\alpha_{\mathrm{0}} }{\mathrm{2}} \\ $$
