Question Number 20541 by tammi last updated on 28/Aug/17
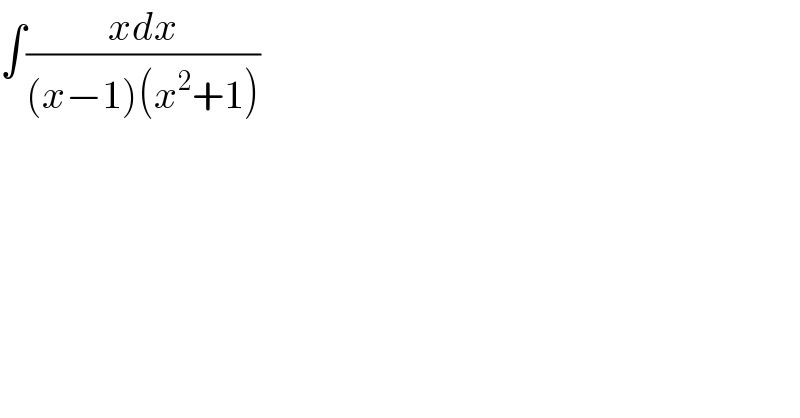
$$\int\frac{{xdx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$
Answered by $@ty@m last updated on 29/Aug/17
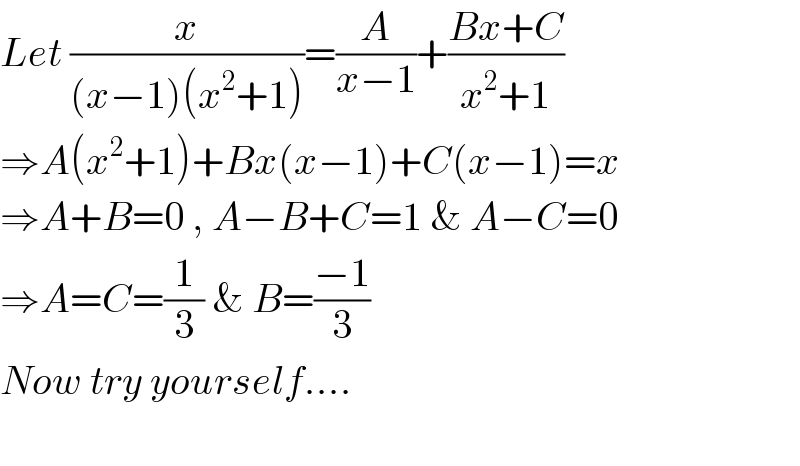
$${Let}\:\frac{{x}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{A}}{{x}−\mathrm{1}}+\frac{{Bx}+{C}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{A}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{Bx}\left({x}−\mathrm{1}\right)+{C}\left({x}−\mathrm{1}\right)={x} \\ $$$$\Rightarrow{A}+{B}=\mathrm{0}\:,\:{A}−{B}+{C}=\mathrm{1}\:\&\:{A}−{C}=\mathrm{0} \\ $$$$\Rightarrow{A}={C}=\frac{\mathrm{1}}{\mathrm{3}}\:\&\:{B}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$${Now}\:{try}\:{yourself}…. \\ $$$$\:\:\:\:\:\: \\ $$
