Question Number 151461 by peter frank last updated on 21/Aug/21
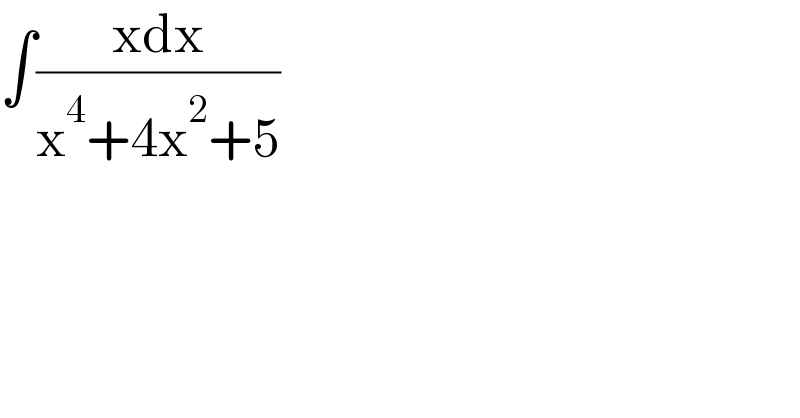
$$\int\frac{\mathrm{xdx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{5}} \\ $$
Answered by puissant last updated on 30/Aug/21

$${I}=\int\frac{{x}}{{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}}{dx}=\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}+\mathrm{5}}{dx} \\ $$$$=\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\mathrm{1}+\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({x}^{\mathrm{2}} +\mathrm{2}\right)+{C} \\ $$$$\:\:\:\:\:\therefore\because\:\:{I}=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({x}^{\mathrm{2}} +\mathrm{2}\right)+{C}.. \\ $$
Commented by peter frank last updated on 21/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
