Question Number 175834 by Linton last updated on 08/Sep/22

$${xe}^{\overset{\mathrm{1}/} {{x}}} =\:{e} \\ $$$${solve}\:{for}\:{x} \\ $$
Commented by mr W last updated on 08/Sep/22
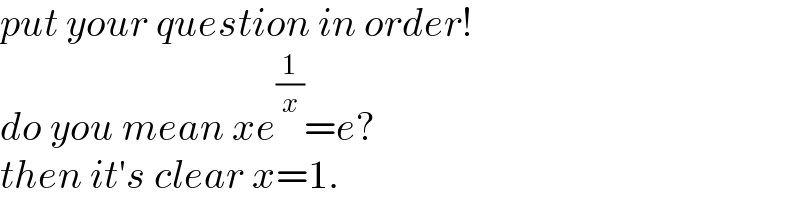
$${put}\:{your}\:{question}\:{in}\:{order}! \\ $$$${do}\:{you}\:{mean}\:{xe}^{\frac{\mathrm{1}}{{x}}} ={e}? \\ $$$${then}\:{it}'{s}\:{clear}\:{x}=\mathrm{1}. \\ $$
Commented by Linton last updated on 08/Sep/22

$${please}\:{show}\:{working} \\ $$
Commented by mr W last updated on 08/Sep/22
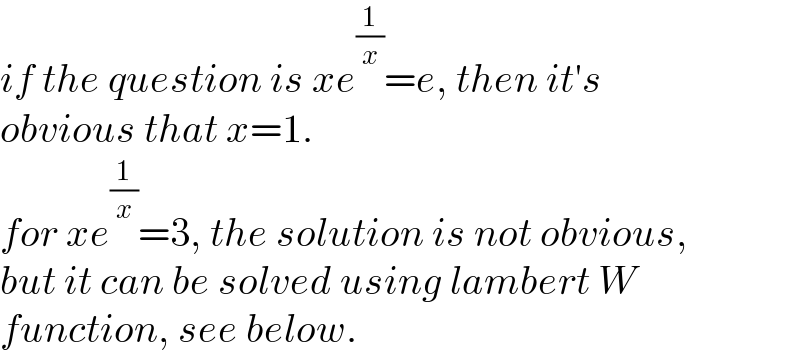
$${if}\:{the}\:{question}\:{is}\:{xe}^{\frac{\mathrm{1}}{{x}}} ={e},\:{then}\:{it}'{s} \\ $$$${obvious}\:{that}\:{x}=\mathrm{1}. \\ $$$${for}\:{xe}^{\frac{\mathrm{1}}{{x}}} =\mathrm{3},\:{the}\:{solution}\:{is}\:{not}\:{obvious}, \\ $$$${but}\:{it}\:{can}\:{be}\:{solved}\:{using}\:{lambert}\:{W} \\ $$$${function},\:{see}\:{below}. \\ $$
Commented by mr W last updated on 08/Sep/22
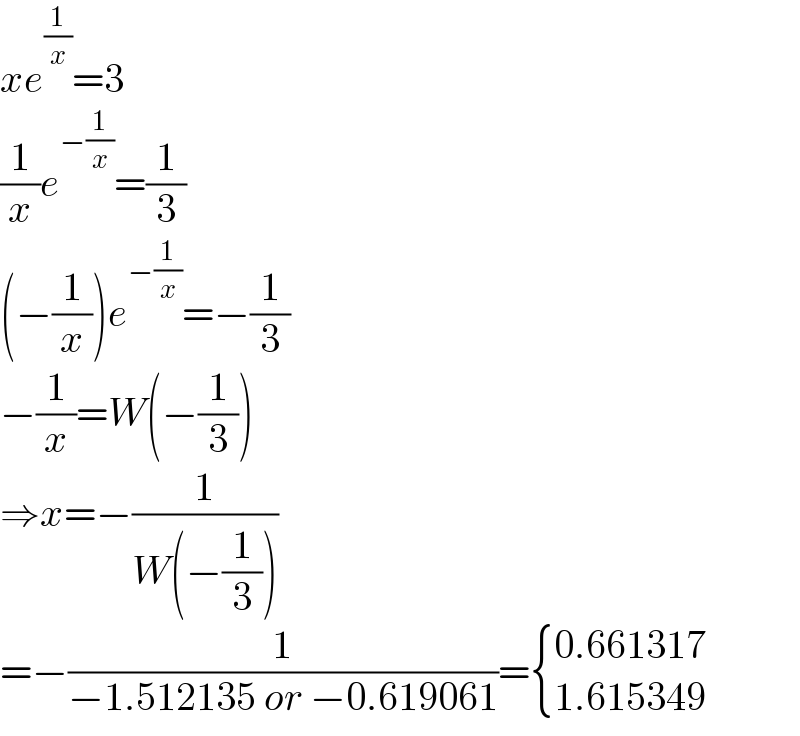
$${xe}^{\frac{\mathrm{1}}{{x}}} =\mathrm{3} \\ $$$$\frac{\mathrm{1}}{{x}}{e}^{−\frac{\mathrm{1}}{{x}}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(−\frac{\mathrm{1}}{{x}}\right){e}^{−\frac{\mathrm{1}}{{x}}} =−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$−\frac{\mathrm{1}}{{x}}={W}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{1}}{{W}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$=−\frac{\mathrm{1}}{−\mathrm{1}.\mathrm{512135}\:{or}\:−\mathrm{0}.\mathrm{619061}}=\begin{cases}{\mathrm{0}.\mathrm{661317}}\\{\mathrm{1}.\mathrm{615349}}\end{cases} \\ $$
