Question Number 181750 by Mastermind last updated on 29/Nov/22

$$\int\mathrm{xe}^{\mathrm{x}^{\mathrm{2}} +\mathrm{x}} \mathrm{dx} \\ $$$$ \\ $$$$. \\ $$
Commented by CElcedricjunior last updated on 29/Nov/22
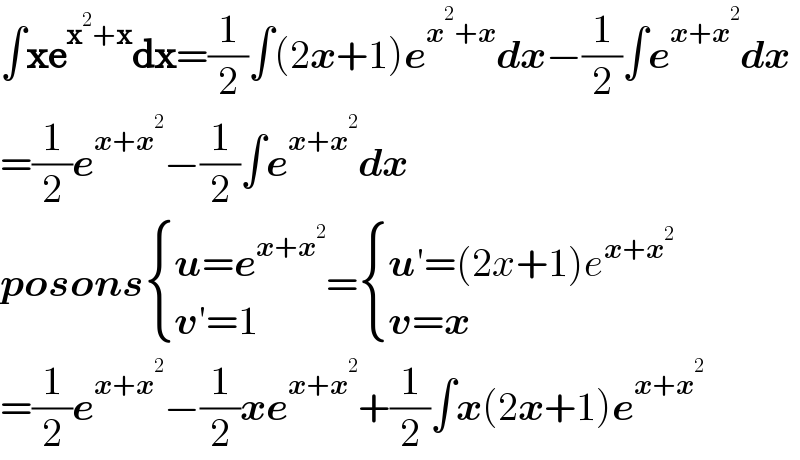
$$\int\boldsymbol{\mathrm{xe}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{e}}^{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{x}}} \boldsymbol{{dx}}−\frac{\mathrm{1}}{\mathrm{2}}\int\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } \boldsymbol{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } −\frac{\mathrm{1}}{\mathrm{2}}\int\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } \boldsymbol{{dx}} \\ $$$$\boldsymbol{{posons\begin{cases}{\boldsymbol{{u}}=\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } }\\{\boldsymbol{{v}}'=\mathrm{1}}\end{cases}}}=\begin{cases}{\boldsymbol{{u}}'=\left(\mathrm{2}{x}+\mathrm{1}\right){e}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } }\\{\boldsymbol{{v}}=\boldsymbol{{x}}}\end{cases} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } −\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{xe}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } +\frac{\mathrm{1}}{\mathrm{2}}\int\boldsymbol{{x}}\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\right)\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} } \\ $$
