Question Number 104104 by bemath last updated on 19/Jul/20
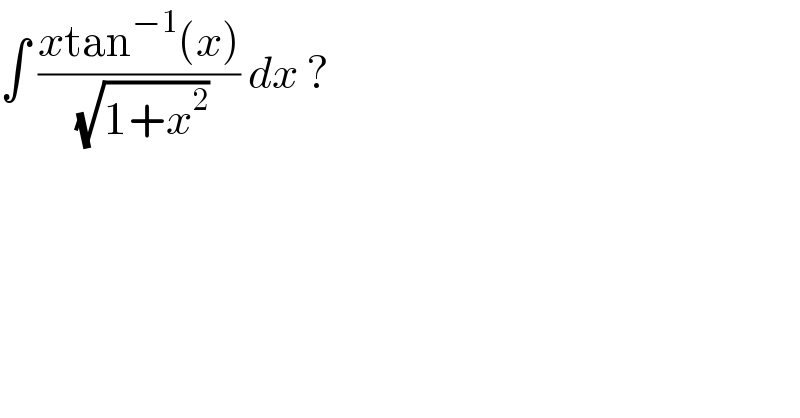
$$\int\:\frac{{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:? \\ $$
Answered by OlafThorendsen last updated on 19/Jul/20
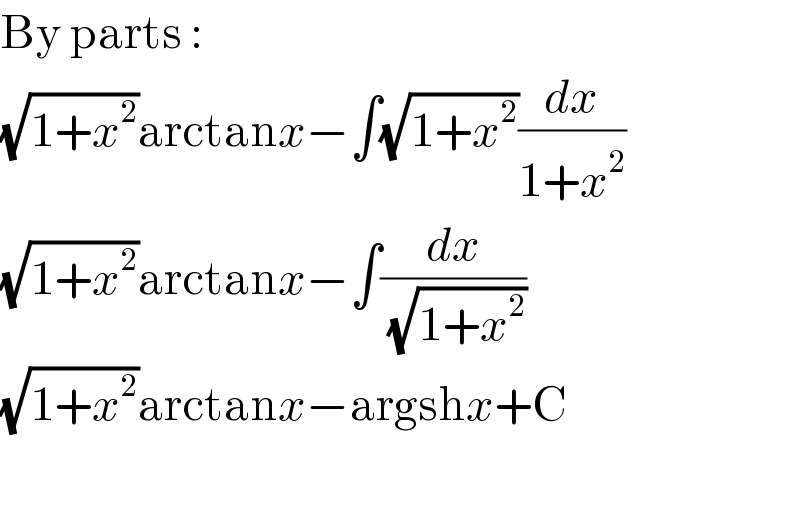
$$\mathrm{By}\:\mathrm{parts}\:: \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\int\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\int\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}{x}−\mathrm{argsh}{x}+\mathrm{C} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 19/Jul/20
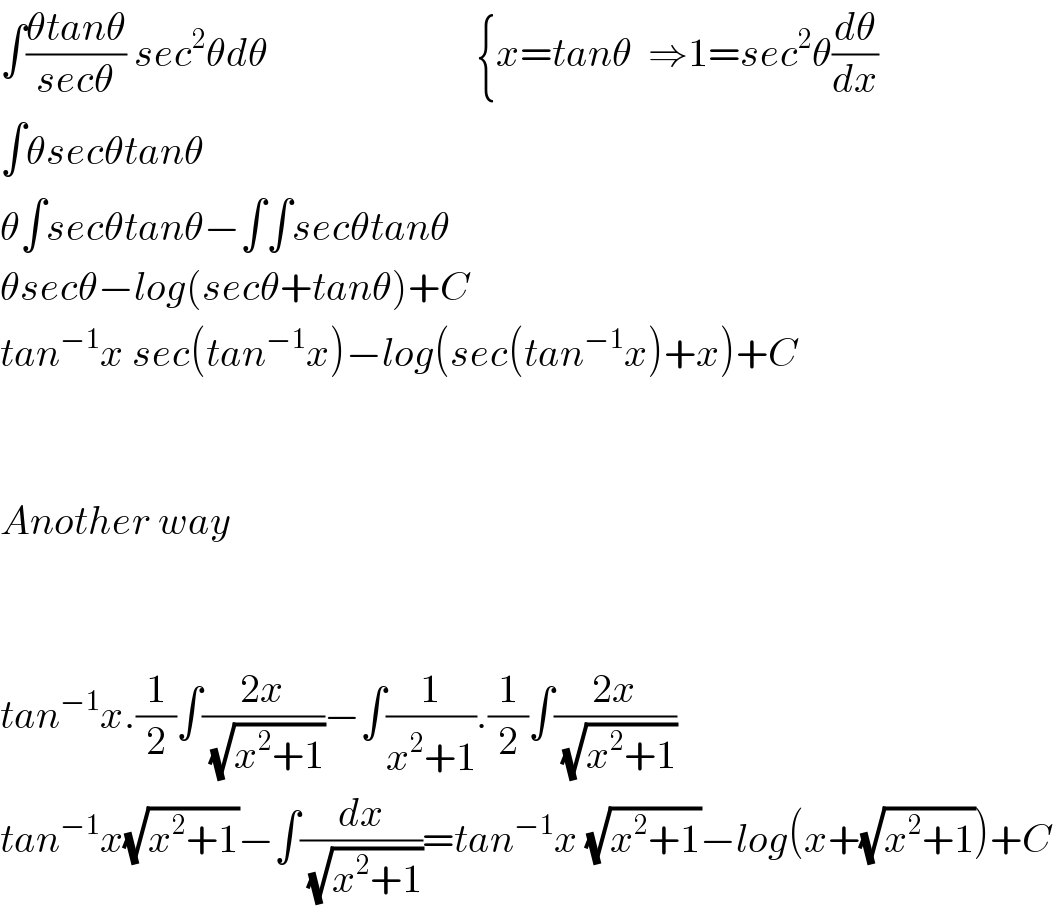
$$\int\frac{\theta{tan}\theta}{{sec}\theta}\:{sec}^{\mathrm{2}} \theta{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}={tan}\theta\:\:\Rightarrow\mathrm{1}={sec}^{\mathrm{2}} \theta\frac{{d}\theta}{{dx}}\right. \\ $$$$\int\theta{sec}\theta{tan}\theta \\ $$$$\theta\int{sec}\theta{tan}\theta−\int\int{sec}\theta{tan}\theta \\ $$$$\theta{sec}\theta−{log}\left({sec}\theta+{tan}\theta\right)+{C} \\ $$$${tan}^{−\mathrm{1}} {x}\:{sec}\left({tan}^{−\mathrm{1}} {x}\right)−{log}\left({sec}\left({tan}^{−\mathrm{1}} {x}\right)+{x}\right)+{C} \\ $$$$ \\ $$$$ \\ $$$${Another}\:{way} \\ $$$$ \\ $$$$ \\ $$$${tan}^{−\mathrm{1}} {x}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${tan}^{−\mathrm{1}} {x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}={tan}^{−\mathrm{1}} {x}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{log}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)+{C} \\ $$
Answered by bobhans last updated on 19/Jul/20
![∫ tan^(−1) (x) d((√(1+x^2 ))) = (√(1+x^2 )) tan^(−1) (x)−∫ ((√(1+x^2 ))/(1+x^2 )) dx = (√(1+x^2 )) tan^(−1) (x)−∫ (dx/( (√(1+x^2 )))) let I_1 = ∫ (dx/( (√(1+x^2 )))) [ x = tan p ] I_1 = ∫ ((sec^2 p)/(sec p)) dp = ∫ sec p dp I_1 = ln ∣sec p + tan p ∣ + c ∴ I = (√(1+x^2 )) tan^(−1) (x)−ln ∣(√(1+x^2 )) +x∣ + c](https://www.tinkutara.com/question/Q104109.png)
$$\int\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:{d}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:=\: \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\int\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:= \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${let}\:{I}_{\mathrm{1}} =\:\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\left[\:{x}\:=\:\mathrm{tan}\:{p}\:\right] \\ $$$${I}_{\mathrm{1}} =\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {p}}{\mathrm{sec}\:{p}}\:{dp}\:=\:\int\:\mathrm{sec}\:{p}\:{dp} \\ $$$${I}_{\mathrm{1}} =\:\mathrm{ln}\:\mid\mathrm{sec}\:{p}\:+\:\mathrm{tan}\:{p}\:\mid\:+\:{c}\: \\ $$$$\therefore\:{I}\:=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{ln}\:\mid\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+{x}\mid\:+\:{c} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 19/Jul/20
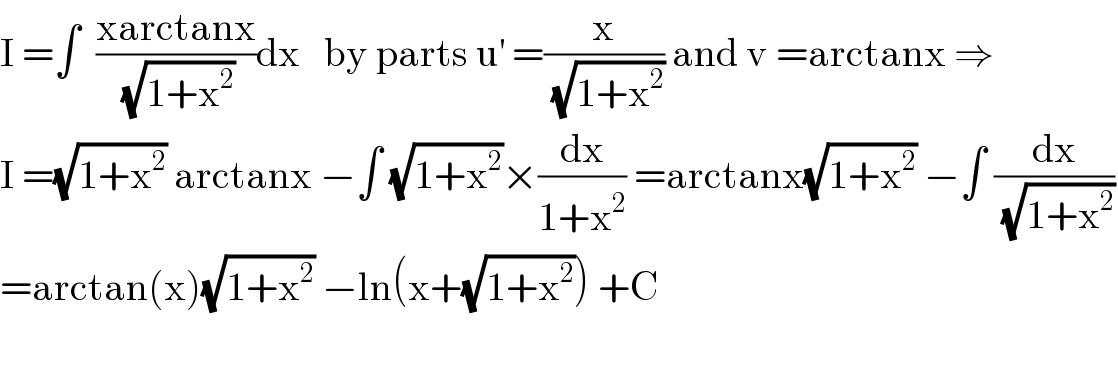
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{xarctanx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{and}\:\mathrm{v}\:=\mathrm{arctanx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{arctanx}\:−\int\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }×\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\mathrm{arctanx}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{arctan}\left(\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:+\mathrm{C} \\ $$$$ \\ $$
