Question Number 14174 by Nayon last updated on 29/May/17
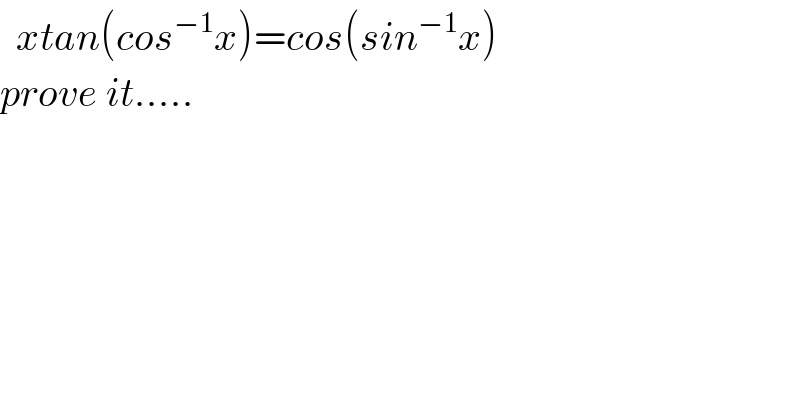
$$\:\:{xtan}\left({cos}^{−\mathrm{1}} {x}\right)={cos}\left({sin}^{−\mathrm{1}} {x}\right) \\ $$$${prove}\:{it}….. \\ $$
Answered by ajfour last updated on 29/May/17
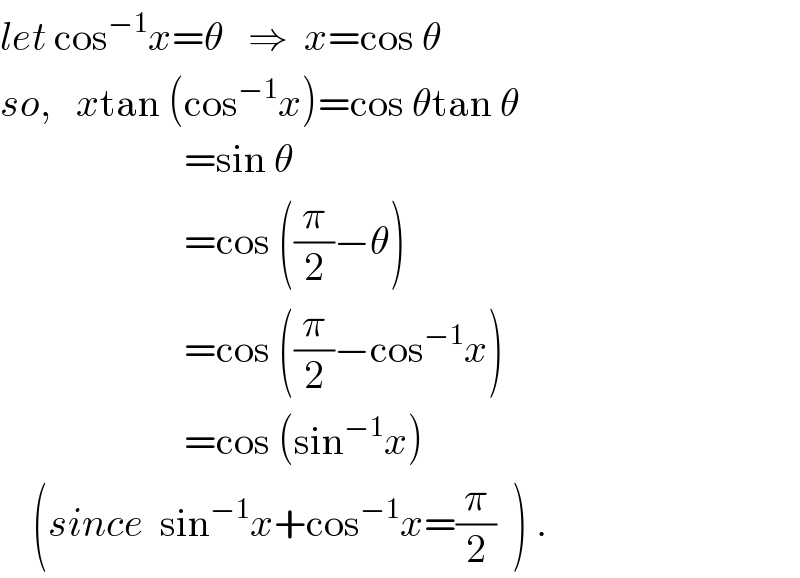
$${let}\:\mathrm{cos}^{−\mathrm{1}} {x}=\theta\:\:\:\Rightarrow\:\:{x}=\mathrm{cos}\:\theta \\ $$$${so},\:\:\:{x}\mathrm{tan}\:\left(\mathrm{cos}^{−\mathrm{1}} {x}\right)=\mathrm{cos}\:\theta\mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{cos}^{−\mathrm{1}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\: \\ $$$$\:\:\:\:\left({since}\:\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{cos}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}}\:\:\right)\:. \\ $$
