Question Number 93512 by Shakhzod last updated on 13/May/20
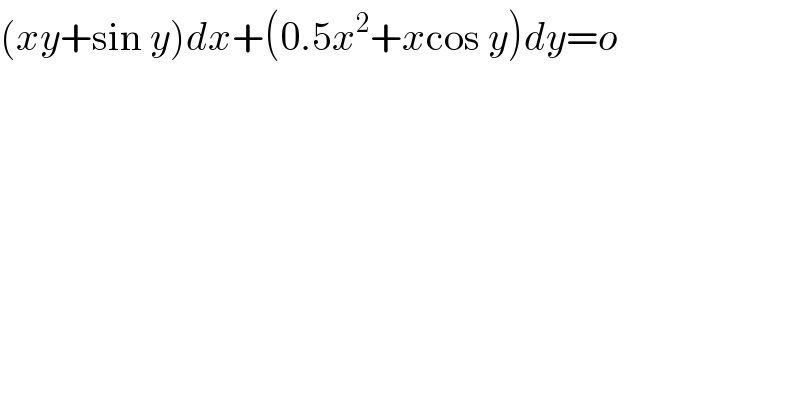
$$\left({xy}+\mathrm{sin}\:{y}\right){dx}+\left(\mathrm{0}.\mathrm{5}{x}^{\mathrm{2}} +{x}\mathrm{cos}\:{y}\right){dy}={o} \\ $$
Commented by i jagooll last updated on 14/May/20
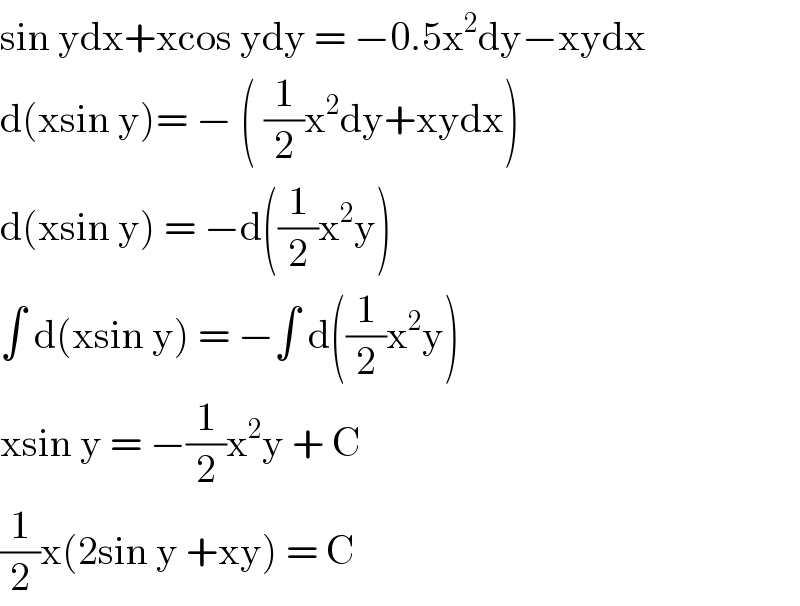
$$\mathrm{sin}\:\mathrm{ydx}+\mathrm{xcos}\:\mathrm{ydy}\:=\:−\mathrm{0}.\mathrm{5x}^{\mathrm{2}} \mathrm{dy}−\mathrm{xydx} \\ $$$$\mathrm{d}\left(\mathrm{xsin}\:\mathrm{y}\right)=\:−\:\left(\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{dy}+\mathrm{xydx}\right) \\ $$$$\mathrm{d}\left(\mathrm{xsin}\:\mathrm{y}\right)\:=\:−\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{y}\right) \\ $$$$\int\:\mathrm{d}\left(\mathrm{xsin}\:\mathrm{y}\right)\:=\:−\int\:\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{y}\right) \\ $$$$\mathrm{xsin}\:\mathrm{y}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{y}\:+\:\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\left(\mathrm{2sin}\:\mathrm{y}\:+\mathrm{xy}\right)\:=\:\mathrm{C}\: \\ $$
Commented by Shakhzod last updated on 13/May/20

$${GoooooD} \\ $$
