Question Number 105158 by bemath last updated on 26/Jul/20
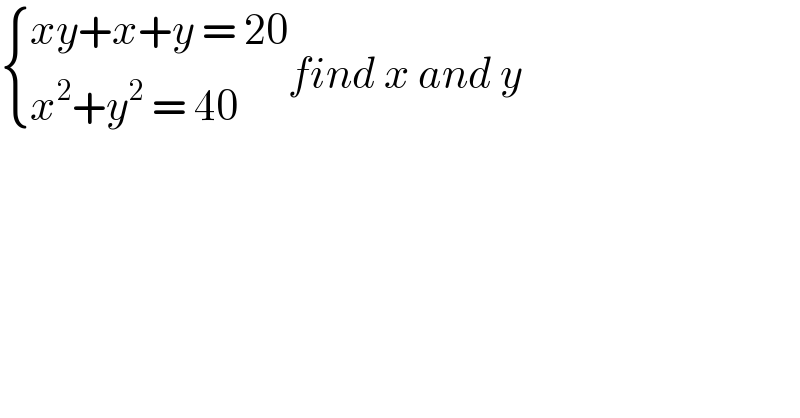
$$\begin{cases}{{xy}+{x}+{y}\:=\:\mathrm{20}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{40}}\end{cases}{find}\:{x}\:{and}\:{y} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jul/20
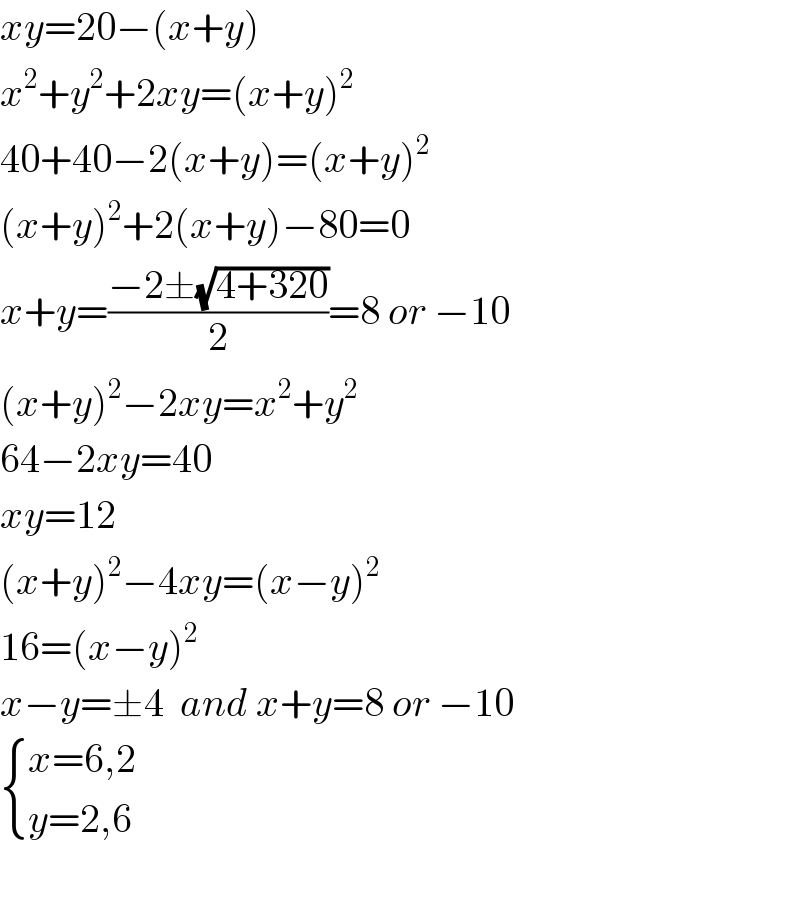
$${xy}=\mathrm{20}−\left({x}+{y}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}=\left({x}+{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{40}+\mathrm{40}−\mathrm{2}\left({x}+{y}\right)=\left({x}+{y}\right)^{\mathrm{2}} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+{y}\right)−\mathrm{80}=\mathrm{0} \\ $$$${x}+{y}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{320}}}{\mathrm{2}}=\mathrm{8}\:{or}\:−\mathrm{10} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\mathrm{64}−\mathrm{2}{xy}=\mathrm{40} \\ $$$${xy}=\mathrm{12} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}=\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{16}=\left({x}−{y}\right)^{\mathrm{2}} \\ $$$${x}−{y}=\pm\mathrm{4}\:\:{and}\:{x}+{y}=\mathrm{8}\:{or}\:−\mathrm{10} \\ $$$$\begin{cases}{{x}=\mathrm{6},\mathrm{2}}\\{{y}=\mathrm{2},\mathrm{6}}\end{cases} \\ $$$$ \\ $$
Answered by bramlex last updated on 26/Jul/20
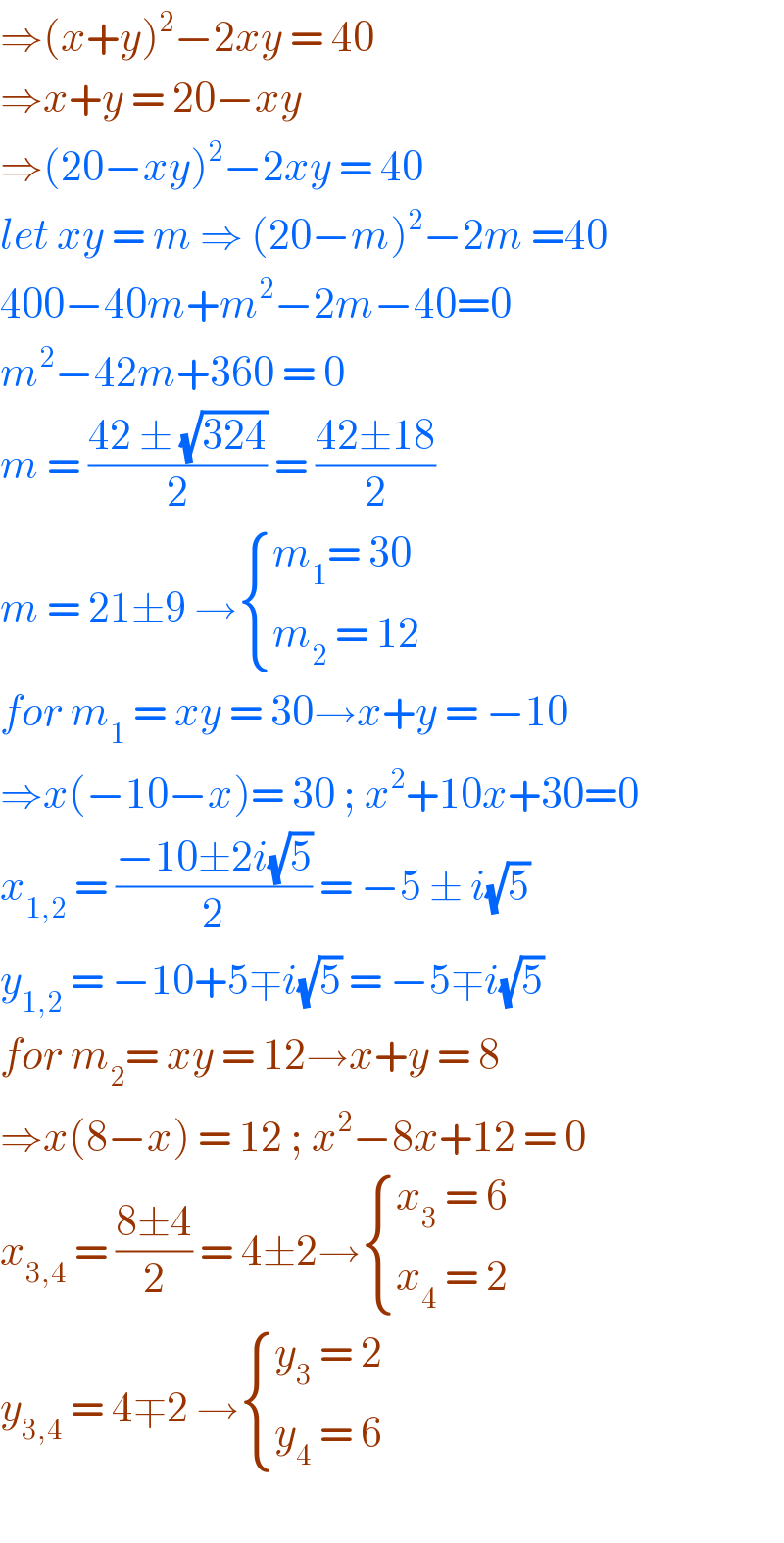
$$\Rightarrow\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\:=\:\mathrm{40} \\ $$$$\Rightarrow{x}+{y}\:=\:\mathrm{20}−{xy}\: \\ $$$$\Rightarrow\left(\mathrm{20}−{xy}\right)^{\mathrm{2}} −\mathrm{2}{xy}\:=\:\mathrm{40} \\ $$$${let}\:{xy}\:=\:{m}\:\Rightarrow\:\left(\mathrm{20}−{m}\right)^{\mathrm{2}} −\mathrm{2}{m}\:=\mathrm{40} \\ $$$$\mathrm{400}−\mathrm{40}{m}+{m}^{\mathrm{2}} −\mathrm{2}{m}−\mathrm{40}=\mathrm{0} \\ $$$${m}^{\mathrm{2}} −\mathrm{42}{m}+\mathrm{360}\:=\:\mathrm{0} \\ $$$${m}\:=\:\frac{\mathrm{42}\:\pm\:\sqrt{\mathrm{324}}}{\mathrm{2}}\:=\:\frac{\mathrm{42}\pm\mathrm{18}}{\mathrm{2}}\: \\ $$$${m}\:=\:\mathrm{21}\pm\mathrm{9}\:\rightarrow\begin{cases}{{m}_{\mathrm{1}} =\:\mathrm{30}}\\{{m}_{\mathrm{2}} \:=\:\mathrm{12}}\end{cases} \\ $$$${for}\:{m}_{\mathrm{1}} \:=\:{xy}\:=\:\mathrm{30}\rightarrow{x}+{y}\:=\:−\mathrm{10} \\ $$$$\Rightarrow{x}\left(−\mathrm{10}−{x}\right)=\:\mathrm{30}\:;\:{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{30}=\mathrm{0} \\ $$$${x}_{\mathrm{1},\mathrm{2}} \:=\:\frac{−\mathrm{10}\pm\mathrm{2}{i}\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:−\mathrm{5}\:\pm\:{i}\sqrt{\mathrm{5}} \\ $$$${y}_{\mathrm{1},\mathrm{2}} \:=\:−\mathrm{10}+\mathrm{5}\mp{i}\sqrt{\mathrm{5}}\:=\:−\mathrm{5}\mp{i}\sqrt{\mathrm{5}} \\ $$$${for}\:{m}_{\mathrm{2}} =\:{xy}\:=\:\mathrm{12}\rightarrow{x}+{y}\:=\:\mathrm{8} \\ $$$$\Rightarrow{x}\left(\mathrm{8}−{x}\right)\:=\:\mathrm{12}\:;\:{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\:=\:\mathrm{0} \\ $$$${x}_{\mathrm{3},\mathrm{4}} \:=\:\frac{\mathrm{8}\pm\mathrm{4}}{\mathrm{2}}\:=\:\mathrm{4}\pm\mathrm{2}\rightarrow\begin{cases}{{x}_{\mathrm{3}} \:=\:\mathrm{6}}\\{{x}_{\mathrm{4}} \:=\:\mathrm{2}}\end{cases}\:\: \\ $$$${y}_{\mathrm{3},\mathrm{4}} \:=\:\mathrm{4}\mp\mathrm{2}\:\rightarrow\begin{cases}{{y}_{\mathrm{3}} \:=\:\mathrm{2}}\\{{y}_{\mathrm{4}} \:=\:\mathrm{6}}\end{cases} \\ $$$$ \\ $$
Answered by behi83417@gmail.com last updated on 26/Jul/20

$$\mathrm{x}+\mathrm{y}=\mathrm{p},\mathrm{xy}=\mathrm{q} \\ $$$$\Rightarrow\begin{cases}{\mathrm{p}+\mathrm{q}=\mathrm{20}}\\{\mathrm{p}^{\mathrm{2}} −\mathrm{2q}=\mathrm{40}\Rightarrow\mathrm{p}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{20}−\mathrm{p}\right)=\mathrm{40}}\end{cases} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} +\mathrm{2p}+\mathrm{1}=\mathrm{81}\Rightarrow\mathrm{p}+\mathrm{1}=\pm\mathrm{9} \\ $$$$\begin{cases}{\mathrm{p}=\mathrm{8},−\mathrm{10}}\\{\mathrm{q}=\mathrm{12},\mathrm{30}}\end{cases} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} −\mathrm{8z}+\mathrm{12}=\mathrm{0}\Rightarrow\mathrm{z}=\mathrm{2},\mathrm{6}\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{2},\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} +\mathrm{10z}+\mathrm{30}=\mathrm{0}\Rightarrow\mathrm{z}=\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{120}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{z}=−\mathrm{5}\pm\mathrm{i}\sqrt{\mathrm{5}}\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(−\mathrm{5}+\mathrm{i}\sqrt{\mathrm{5}},−\mathrm{5}−\mathrm{i}\sqrt{\mathrm{5}}\right)\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 26/Jul/20
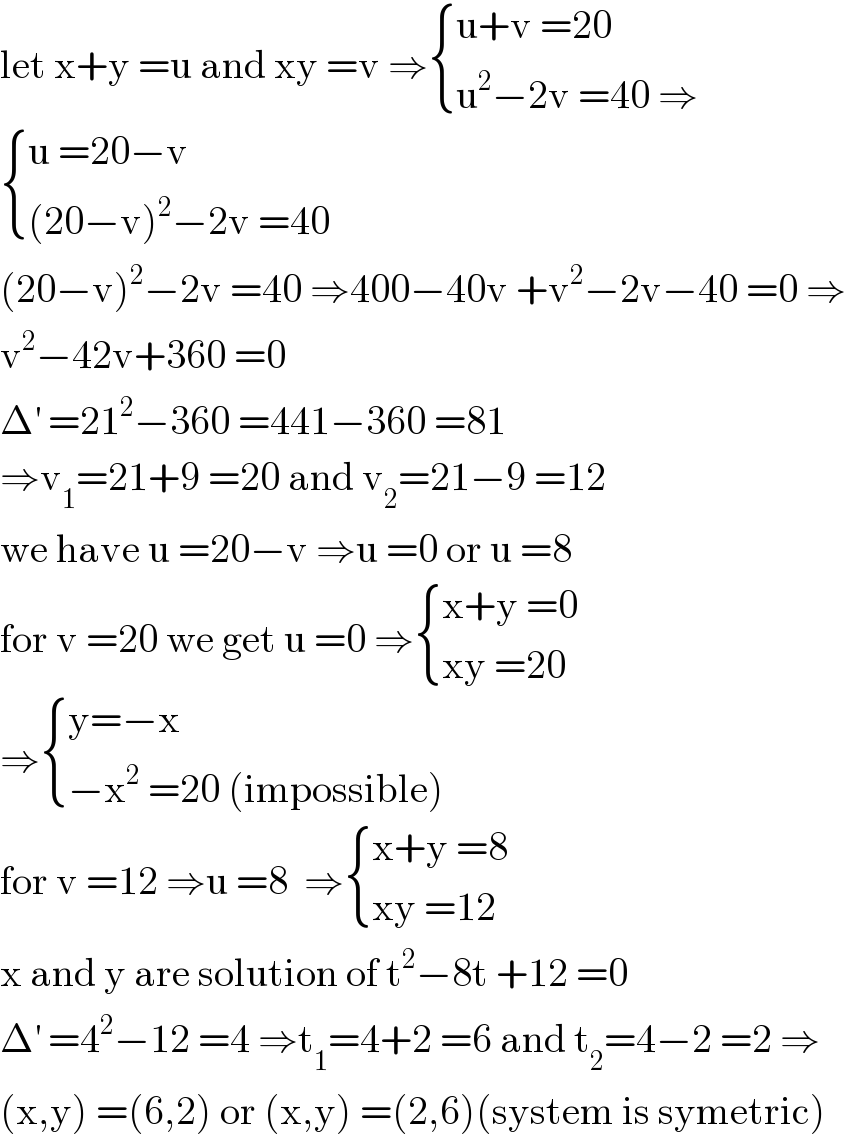
$$\mathrm{let}\:\mathrm{x}+\mathrm{y}\:=\mathrm{u}\:\mathrm{and}\:\mathrm{xy}\:=\mathrm{v}\:\Rightarrow\begin{cases}{\mathrm{u}+\mathrm{v}\:=\mathrm{20}}\\{\mathrm{u}^{\mathrm{2}} −\mathrm{2v}\:=\mathrm{40}\:\Rightarrow}\end{cases} \\ $$$$\begin{cases}{\mathrm{u}\:=\mathrm{20}−\mathrm{v}}\\{\left(\mathrm{20}−\mathrm{v}\right)^{\mathrm{2}} −\mathrm{2v}\:=\mathrm{40}}\end{cases} \\ $$$$\left(\mathrm{20}−\mathrm{v}\right)^{\mathrm{2}} −\mathrm{2v}\:=\mathrm{40}\:\Rightarrow\mathrm{400}−\mathrm{40v}\:+\mathrm{v}^{\mathrm{2}} −\mathrm{2v}−\mathrm{40}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{v}^{\mathrm{2}} −\mathrm{42v}+\mathrm{360}\:=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{21}^{\mathrm{2}} −\mathrm{360}\:=\mathrm{441}−\mathrm{360}\:=\mathrm{81} \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{1}} =\mathrm{21}+\mathrm{9}\:=\mathrm{20}\:\mathrm{and}\:\mathrm{v}_{\mathrm{2}} =\mathrm{21}−\mathrm{9}\:=\mathrm{12} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{u}\:=\mathrm{20}−\mathrm{v}\:\Rightarrow\mathrm{u}\:=\mathrm{0}\:\mathrm{or}\:\mathrm{u}\:=\mathrm{8} \\ $$$$\mathrm{for}\:\mathrm{v}\:=\mathrm{20}\:\mathrm{we}\:\mathrm{get}\:\mathrm{u}\:=\mathrm{0}\:\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}\:=\mathrm{0}}\\{\mathrm{xy}\:=\mathrm{20}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{y}=−\mathrm{x}}\\{−\mathrm{x}^{\mathrm{2}} \:=\mathrm{20}\:\left(\mathrm{impossible}\right)}\end{cases} \\ $$$$\mathrm{for}\:\mathrm{v}\:=\mathrm{12}\:\Rightarrow\mathrm{u}\:=\mathrm{8}\:\:\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}\:=\mathrm{8}}\\{\mathrm{xy}\:=\mathrm{12}}\end{cases} \\ $$$$\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{are}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{t}^{\mathrm{2}} −\mathrm{8t}\:+\mathrm{12}\:=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{4}^{\mathrm{2}} −\mathrm{12}\:=\mathrm{4}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{4}+\mathrm{2}\:=\mathrm{6}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\mathrm{4}−\mathrm{2}\:=\mathrm{2}\:\Rightarrow \\ $$$$\left(\mathrm{x},\mathrm{y}\right)\:=\left(\mathrm{6},\mathrm{2}\right)\:\mathrm{or}\:\left(\mathrm{x},\mathrm{y}\right)\:=\left(\mathrm{2},\mathrm{6}\right)\left(\mathrm{system}\:\mathrm{is}\:\mathrm{symetric}\right) \\ $$
