Question Number 182534 by Mastermind last updated on 10/Dec/22
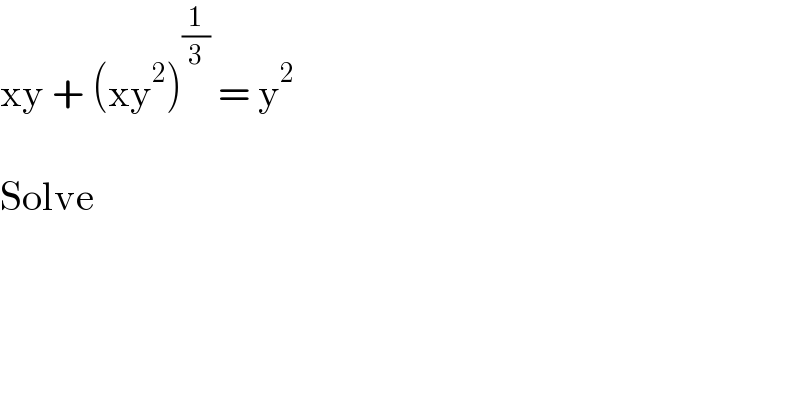
$$\mathrm{xy}\:+\:\left(\mathrm{xy}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\:\mathrm{y}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$
Commented by Frix last updated on 10/Dec/22
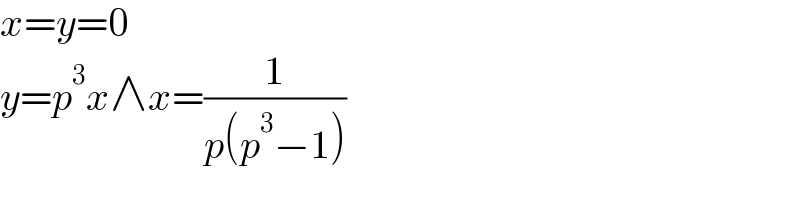
$${x}={y}=\mathrm{0} \\ $$$${y}={p}^{\mathrm{3}} {x}\wedge{x}=\frac{\mathrm{1}}{{p}\left({p}^{\mathrm{3}} −\mathrm{1}\right)} \\ $$
Commented by mr W last updated on 11/Dec/22
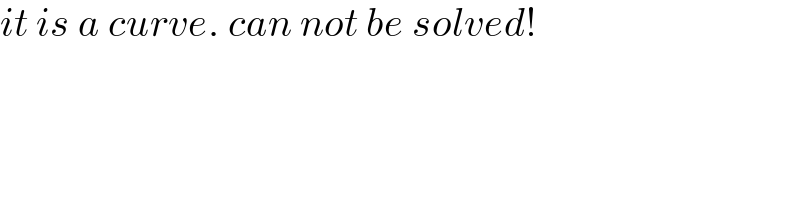
$${it}\:{is}\:{a}\:{curve}.\:{can}\:{not}\:{be}\:{solved}! \\ $$
Commented by Frix last updated on 11/Dec/22

$$\mathrm{Yes}\:\mathrm{of}\:\mathrm{vourse}\:\mathrm{with}\:{p}\:\mathrm{as}\:\mathrm{parameter}.\:\mathrm{I}\:\mathrm{tbought} \\ $$$$\mathrm{this}\:\mathrm{was}\:\mathrm{obvious}. \\ $$
Answered by manxsol last updated on 11/Dec/22

$${Right}\:{Frix},\:{develop}\:{your}\: \\ $$$${approach}\:{and}\:{put}\:{the} \\ $$$$\:{condition}\:{for}\:{p}\:{and}\: \\ $$$${solution}\:{set}. \\ $$$${Thanks}\:{Sir}\:{W} \\ $$$$\:{for}\:{correction} \\ $$$$ \\ $$$${PROCESS}:\:\:{parameterized} \\ $$$$\:{curve} \\ $$$${not}\:{solved} \\ $$$$ \\ $$$${if}\:\:{y}={x}\nRightarrow\:\:{x}^{\mathrm{2}} +{x}={x}^{\mathrm{2}} \\ $$$${condition}\:\:\:\:{y}\neq{x} \\ $$$$ \\ $$$${y}={p}^{\mathrm{3}} {x} \\ $$$${x}\left({p}^{\mathrm{3}} {x}\right)+\left({xp}^{\mathrm{6}} {x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} ={p}^{\mathrm{6}} {x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {p}^{\mathrm{3}} +{xp}^{\mathrm{2}} ={p}^{\mathrm{6}} {x}^{\mathrm{2}} \\ $$$${x}=\mathrm{0}\Rightarrow{y}=\mathrm{0}\:\:\:\:\:\left(\mathrm{0};\mathrm{0}\right) \\ $$$${xp}^{\mathrm{3}} +{p}^{\mathrm{2}} ={p}^{\mathrm{6}} {x} \\ $$$${x}=\frac{{p}^{\mathrm{2}} }{{p}^{\mathrm{6}} −{p}^{\mathrm{3}} }=\frac{\mathrm{1}}{{p}\left({p}^{\mathrm{3}} −\mathrm{1}\right)} \\ $$$${parameterized} \\ $$$${f}\left({p}\right)=\left\{\left(\mathrm{0};\mathrm{0}\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{{p}\left({p}^{\mathrm{3}} −\mathrm{1}\right)};\:\:\frac{{p}^{\mathrm{2}} }{\left({p}^{\mathrm{3}} −\mathrm{1}\right)}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}\neq\mathrm{1}\:{p}\neq\mathrm{0}\:\: \\ $$
Commented by Mastermind last updated on 11/Dec/22
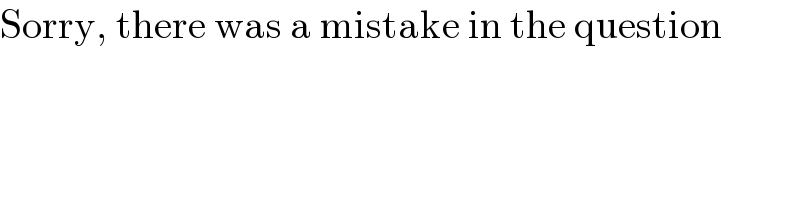
$$\mathrm{Sorry},\:\mathrm{there}\:\mathrm{was}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question} \\ $$
Commented by Mastermind last updated on 11/Dec/22
$$\mathrm{Check}\:\mathrm{the}\:\mathrm{next}\:\mathrm{slide}\:\mathrm{for}\:\mathrm{new}\:\mathrm{ques}. \\ $$$$\mathrm{l}'\mathrm{m}\:\mathrm{sorry} \\ $$
Commented by manxsol last updated on 11/Dec/22
$${has}\:{not}\:{been}\:{resolved}, \\ $$$$\:{has}\:{been}\:{parameterized} \\ $$
