Question Number 96140 by Farruxjano last updated on 30/May/20
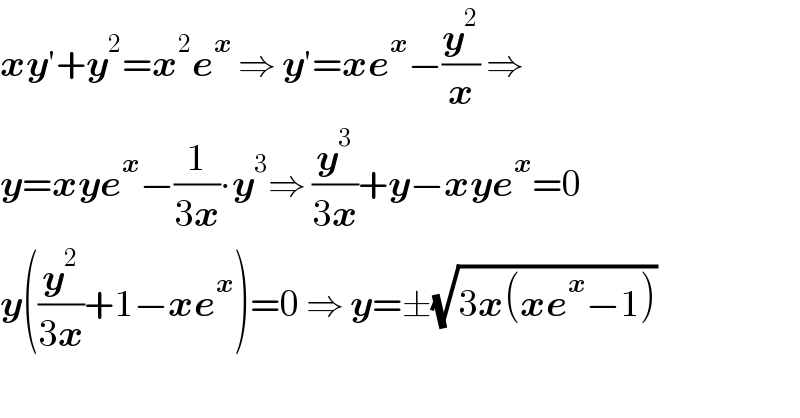
$$\boldsymbol{{xy}}'+\boldsymbol{{y}}^{\mathrm{2}} =\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{e}}^{\boldsymbol{{x}}} \:\Rightarrow\:\boldsymbol{{y}}'=\boldsymbol{{xe}}^{\boldsymbol{{x}}} −\frac{\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}}\:\Rightarrow \\ $$$$\boldsymbol{{y}}=\boldsymbol{{xye}}^{\boldsymbol{{x}}} −\frac{\mathrm{1}}{\mathrm{3}\boldsymbol{{x}}}\centerdot\boldsymbol{{y}}^{\mathrm{3}} \Rightarrow\:\frac{\boldsymbol{{y}}^{\mathrm{3}} }{\mathrm{3}\boldsymbol{{x}}}+\boldsymbol{{y}}−\boldsymbol{{xye}}^{\boldsymbol{{x}}} =\mathrm{0} \\ $$$$\boldsymbol{{y}}\left(\frac{\boldsymbol{{y}}^{\mathrm{2}} }{\mathrm{3}\boldsymbol{{x}}}+\mathrm{1}−\boldsymbol{{xe}}^{\boldsymbol{{x}}} \right)=\mathrm{0}\:\Rightarrow\:\boldsymbol{{y}}=\pm\sqrt{\mathrm{3}\boldsymbol{{x}}\left(\boldsymbol{{xe}}^{\boldsymbol{{x}}} −\mathrm{1}\right)} \\ $$
Commented by john santu last updated on 30/May/20
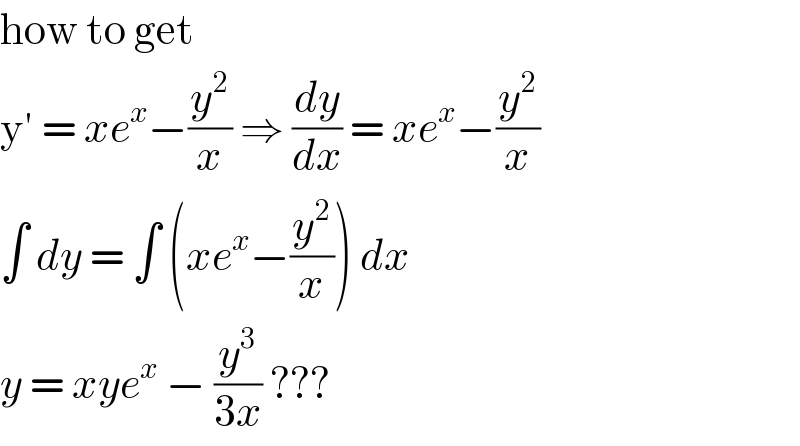
$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\: \\ $$$$\mathrm{y}'\:=\:{xe}^{{x}} −\frac{{y}^{\mathrm{2}} }{{x}}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{xe}^{{x}} −\frac{{y}^{\mathrm{2}} }{{x}} \\ $$$$\int\:{dy}\:=\:\int\:\left({xe}^{{x}} −\frac{{y}^{\mathrm{2}} }{{x}}\right)\:{dx}\: \\ $$$${y}\:=\:{xye}^{{x}} \:−\:\frac{{y}^{\mathrm{3}} }{\mathrm{3}{x}}\:???\: \\ $$
Commented by mr W last updated on 30/May/20

$${please}\:{post}\:{your}\:{answer}\:{in}\:{the}\:{same} \\ $$$${thread}\:{as}\:{the}\:{question}\:{itself}.\:{don}'{t} \\ $$$${open}\:{a}\:{new}\:{one}! \\ $$
Commented by mr W last updated on 30/May/20

$${besides},\:{your}\:{solution}\:{is}\:{wrong}. \\ $$
Commented by Farruxjano last updated on 30/May/20

$$\mathrm{I}\:\mathrm{tried},\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{was}\:\mathrm{going}\:\mathrm{to}\:\mathrm{know}\:\mathrm{the}\:\mathrm{solution} \\ $$
Commented by mr W last updated on 30/May/20

$${it}\:{is}\:{absolutely}\:{ok}\:{when}\:{you}\:{don}'{t} \\ $$$${know}\:{how}\:{to}\:{solve}\:{a}\:{question}.\:{i}\:{also} \\ $$$${don}'{t}\:{know}\:{how}\:{to}\:{solve}\:{it}.\:{then}\:{i} \\ $$$${keep}\:{being}\:{silent}\:{and}\:{look}\:{how}\:{the} \\ $$$${others}\:{solve}\:{it}\:{and}\:{learn}\:{from}\:{them}. \\ $$
Answered by john santu last updated on 30/May/20

$$\mathrm{it}\:\mathrm{impossible} \\ $$
