Question Number 101841 by bemath last updated on 05/Jul/20
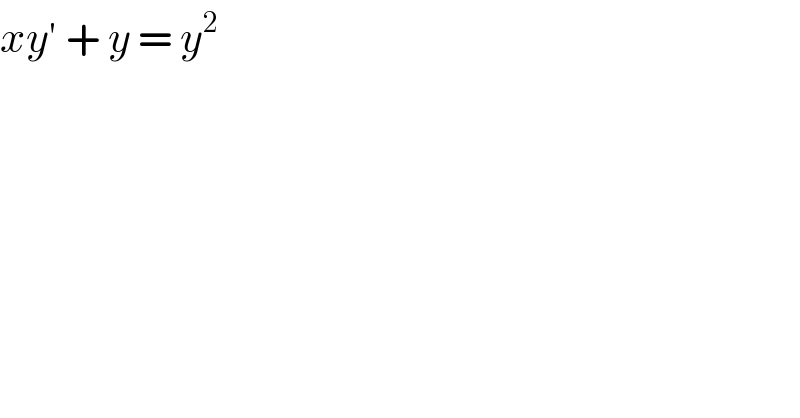
$${xy}'\:+\:{y}\:=\:{y}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 05/Jul/20
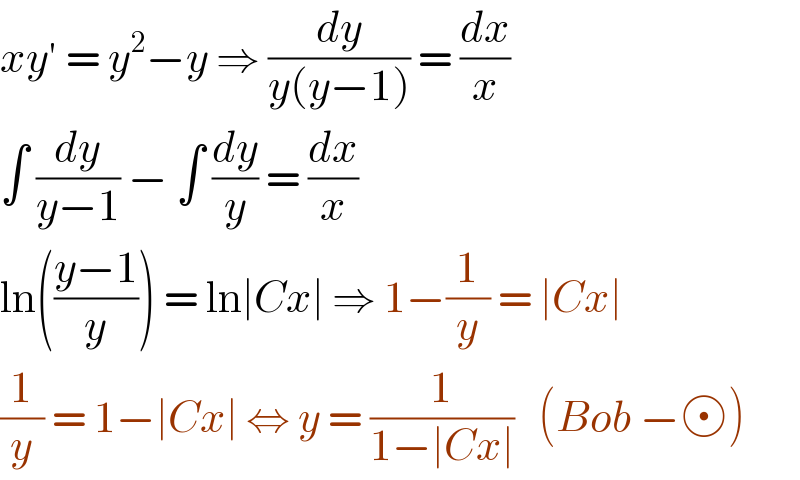
$${xy}'\:=\:{y}^{\mathrm{2}} −{y}\:\Rightarrow\:\frac{{dy}}{{y}\left({y}−\mathrm{1}\right)}\:=\:\frac{{dx}}{{x}} \\ $$$$\int\:\frac{{dy}}{{y}−\mathrm{1}}\:−\:\int\:\frac{{dy}}{{y}}\:=\:\frac{{dx}}{{x}} \\ $$$$\mathrm{ln}\left(\frac{{y}−\mathrm{1}}{{y}}\right)\:=\:\mathrm{ln}\mid{Cx}\mid\:\Rightarrow\:\mathrm{1}−\frac{\mathrm{1}}{{y}}\:=\:\mid{Cx}\mid\: \\ $$$$\frac{\mathrm{1}}{{y}}\:=\:\mathrm{1}−\mid{Cx}\mid\:\Leftrightarrow\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mid{Cx}\mid}\:\:\:\left({Bob}\:− \right) \\ $$
Commented by bemath last updated on 05/Jul/20
macho......^o^
