Question Number 93039 by i jagooll last updated on 10/May/20
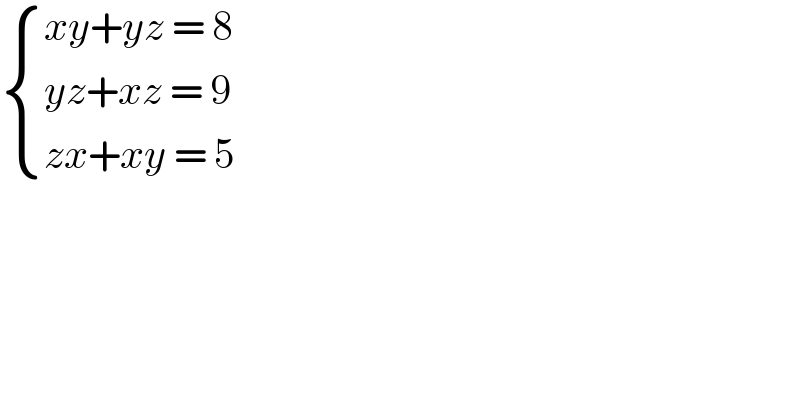
$$\begin{cases}{{xy}+{yz}\:=\:\mathrm{8}}\\{{yz}+{xz}\:=\:\mathrm{9}}\\{{zx}+{xy}\:=\:\mathrm{5}}\end{cases} \\ $$
Commented by i jagooll last updated on 10/May/20
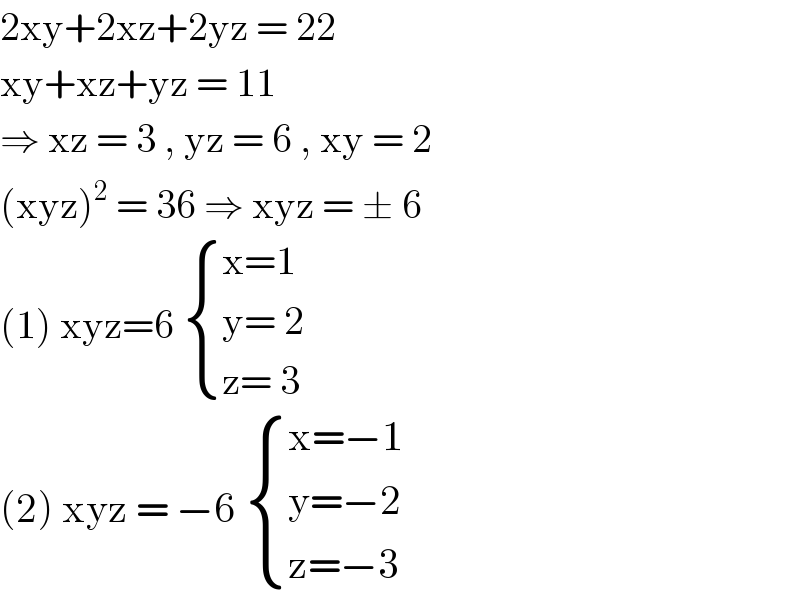
$$\mathrm{2xy}+\mathrm{2xz}+\mathrm{2yz}\:=\:\mathrm{22} \\ $$$$\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\:=\:\mathrm{11} \\ $$$$\Rightarrow\:\mathrm{xz}\:=\:\mathrm{3}\:,\:\mathrm{yz}\:=\:\mathrm{6}\:,\:\mathrm{xy}\:=\:\mathrm{2}\: \\ $$$$\left(\mathrm{xyz}\right)^{\mathrm{2}} \:=\:\mathrm{36}\:\Rightarrow\:\mathrm{xyz}\:=\:\pm\:\mathrm{6} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{xyz}=\mathrm{6}\:\begin{cases}{\mathrm{x}=\mathrm{1}}\\{\mathrm{y}=\:\mathrm{2}}\\{\mathrm{z}=\:\mathrm{3}}\end{cases} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{xyz}\:=\:−\mathrm{6}\:\begin{cases}{\mathrm{x}=−\mathrm{1}}\\{\mathrm{y}=−\mathrm{2}}\\{\mathrm{z}=−\mathrm{3}}\end{cases} \\ $$
