Question Number 26299 by d.monhbayr@gmail.com last updated on 23/Dec/17

$${y}=\frac{\mathrm{1}+{e}^{{x}} }{\mathrm{1}−{e}^{{x}} } \\ $$$${y}'=? \\ $$
Commented by abdo imad last updated on 24/Dec/17
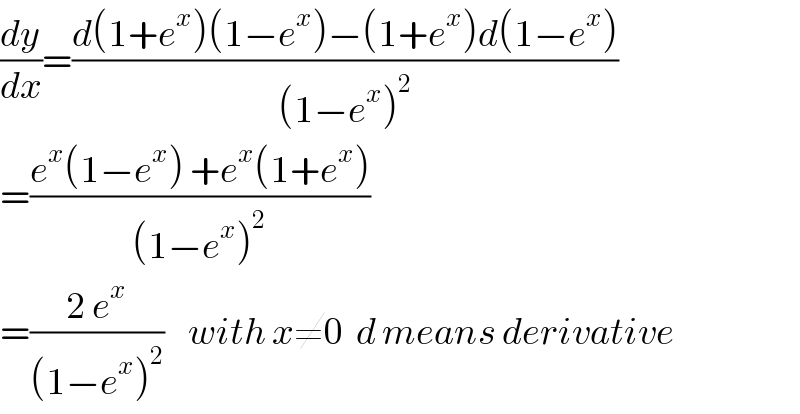
$$\frac{{dy}}{{dx}}=\frac{{d}\left(\mathrm{1}+{e}^{{x}} \right)\left(\mathrm{1}−{e}^{{x}} \right)−\left(\mathrm{1}+{e}^{{x}} \right){d}\left(\mathrm{1}−{e}^{{x}} \right)}{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$$=\frac{{e}^{{x}} \left(\mathrm{1}−{e}^{{x}} \right)\:+{e}^{{x}} \left(\mathrm{1}+{e}^{{x}} \right)}{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}\:{e}^{{x}} }{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} }\:\:\:\:{with}\:{x}\neq\mathrm{0}\:\:{d}\:{means}\:{derivative} \\ $$
