Menu Close

y-1-x-2-x-1-y-2-0-find-dy-dx-

Tinku Tara 0 Comments
Pin




Question Number 123086 by aurpeyz last updated on 22/Nov/20
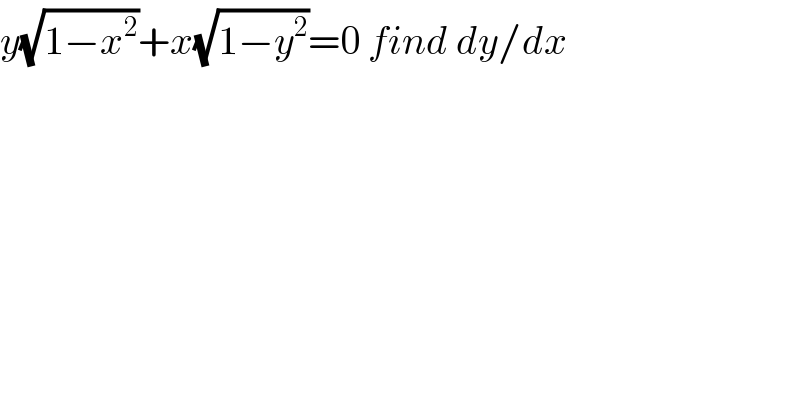
y(√(1−x^2 ))+x(√(1−y^2 ))=0 find dy/dx
$${y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }=\mathrm{0}\:{find}\:{dy}/{dx} \\ $$
Commented by liberty last updated on 23/Nov/20
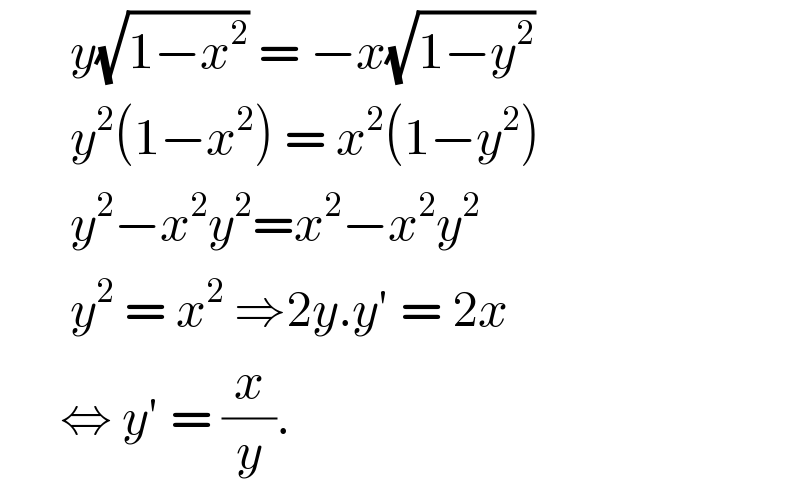
y(√(1−x^2 )) = −x(√(1−y^2 )) y^2 (1−x^2 ) = x^2 (1−y^2 ) y^2 −x^2 y^2 =x^2 −x^2 y^2 y^2 = x^2 ⇒2y.y′ = 2x ⇔ y′ = (x/y).
$$\:\:\:\:\:\:\:{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:−{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\:{y}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:=\:{x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:{y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} ={x}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{y}^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{y}.{y}'\:=\:\mathrm{2}{x}\: \\ $$$$\:\:\:\:\:\:\Leftrightarrow\:{y}'\:=\:\frac{{x}}{{y}}.\: \\ $$
Answered by Dwaipayan Shikari last updated on 22/Nov/20
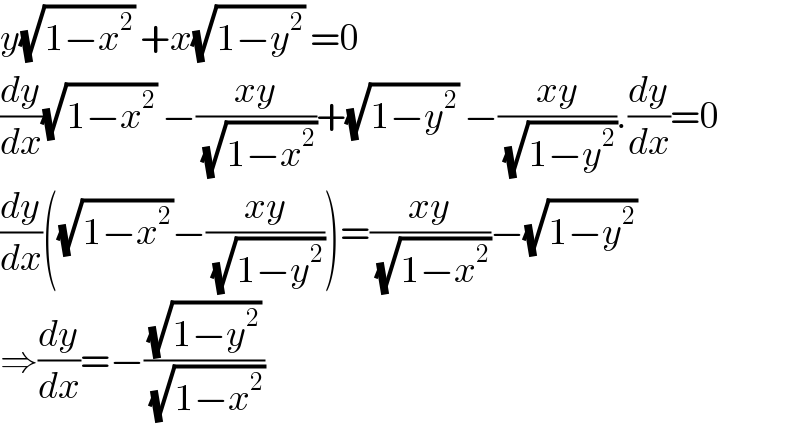
y(√(1−x^2 )) +x(√(1−y^2 )) =0 (dy/dx)(√(1−x^2 )) −((xy)/( (√(1−x^2 ))))+(√(1−y^2 )) −((xy)/( (√(1−y^2 )))).(dy/dx)=0 (dy/dx)((√(1−x^2 ))−((xy)/( (√(1−y^2 )))))=((xy)/( (√(1−x^2 ))))−(√(1−y^2 )) ⇒(dy/dx)=−((√(1−y^2 ))/( (√(1−x^2 ))))
$${y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\frac{{xy}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\:−\frac{{xy}}{\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}.\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\frac{{xy}}{\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}\right)=\frac{{xy}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\sqrt{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=−\frac{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Answered by mathmax by abdo last updated on 22/Nov/20
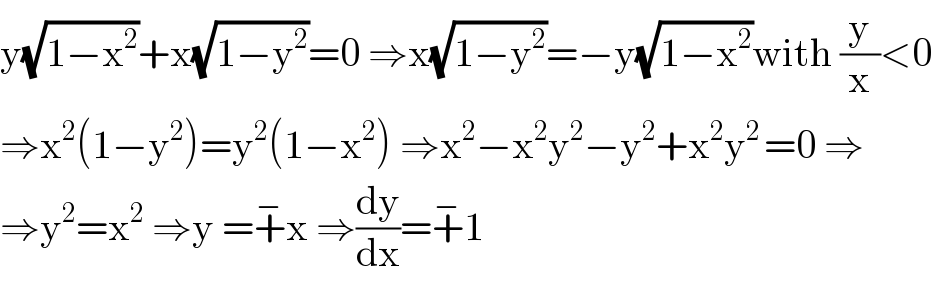
y(√(1−x^2 ))+x(√(1−y^2 ))=0 ⇒x(√(1−y^2 ))=−y(√(1−x^2 ))with (y/x)<0 ⇒x^2 (1−y^2 )=y^2 (1−x^2 ) ⇒x^2 −x^2 y^2 −y^2 +x^2 y^(2 ) =0 ⇒ ⇒y^2 =x^2 ⇒y =+^− x ⇒(dy/dx)=+^− 1
$$\mathrm{y}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }+\mathrm{x}\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow\mathrm{x}\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }=−\mathrm{y}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{with}\:\frac{\mathrm{y}}{\mathrm{x}}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)=\mathrm{y}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}\:} =\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{y}\:=\overset{−} {+}\mathrm{x}\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\overset{−} {+}\mathrm{1} \\ $$
Answered by aurpeyz last updated on 22/Nov/20
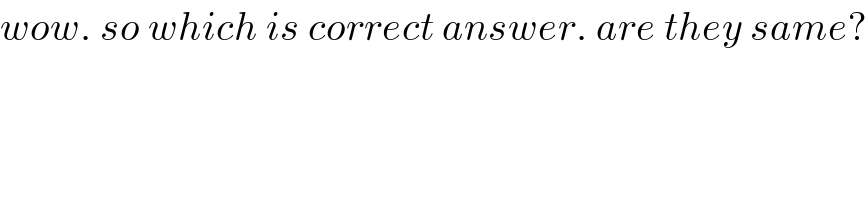
wow. so which is correct answer. are they same?
$${wow}.\:{so}\:{which}\:{is}\:{correct}\:{answer}.\:{are}\:{they}\:{same}? \\ $$
Commented by mathmax by abdo last updated on 23/Nov/20
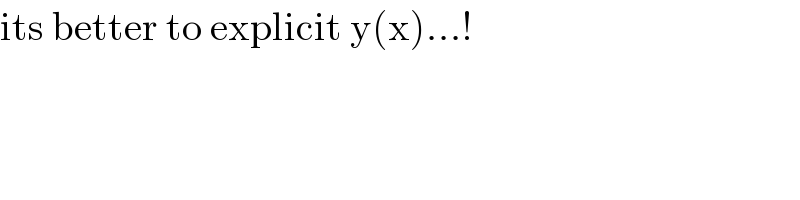
its better to explicit y(x)...!
$$\mathrm{its}\:\mathrm{better}\:\mathrm{to}\:\mathrm{explicit}\:\mathrm{y}\left(\mathrm{x}\right)…! \\ $$
Answered by MJS_new last updated on 23/Nov/20
y(√(1−x^2 ))+x(√(1−y^2 ))=0 let x>0∧y<0 [it makes no difference to x<0∧y>0] x(√(1−y^2 ))=−y(√(1−x^2 )) x^2 (1−y^2 )=y^2 (1−x^2 ) x^2 =y^2 ⇒ y=−x ⇒ (dy/dx)=−1
$${y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{let}\:{x}>\mathrm{0}\wedge{y}<\mathrm{0}\:\left[\mathrm{it}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{difference}\:\mathrm{to}\:{x}<\mathrm{0}\wedge{y}>\mathrm{0}\right] \\ $$$${x}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }=−{y}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}−{y}^{\mathrm{2}} \right)={y}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} ={y}^{\mathrm{2}} \:\Rightarrow\:{y}=−{x} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=−\mathrm{1} \\ $$
Commented by benjo_mathlover last updated on 23/Nov/20
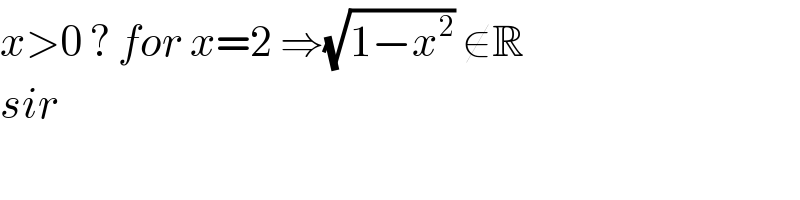
x>0 ? for x=2 ⇒(√(1−x^2 )) ∉R sir
$${x}>\mathrm{0}\:?\:{for}\:{x}=\mathrm{2}\:\Rightarrow\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\notin\mathbb{R}\: \\ $$$${sir} \\ $$
Commented by MJS_new last updated on 23/Nov/20
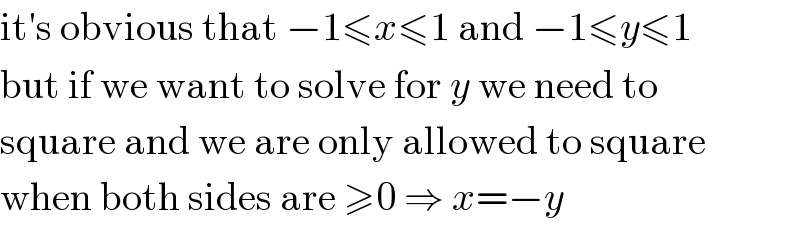
it′s obvious that −1≤x≤1 and −1≤y≤1 but if we want to solve for y we need to square and we are only allowed to square when both sides are ≥0 ⇒ x=−y
$$\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{that}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\:\mathrm{and}\:−\mathrm{1}\leqslant{y}\leqslant\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{want}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{y}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to} \\ $$$$\mathrm{square}\:\mathrm{and}\:\mathrm{we}\:\mathrm{are}\:\mathrm{only}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{square} \\ $$$$\mathrm{when}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{are}\:\geqslant\mathrm{0}\:\Rightarrow\:{x}=−{y} \\ $$
Commented by benjo_mathlover last updated on 23/Nov/20
oo yes. i agree sir
$${oo}\:{yes}.\:{i}\:{agree}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *