Question Number 99992 by bemath last updated on 24/Jun/20
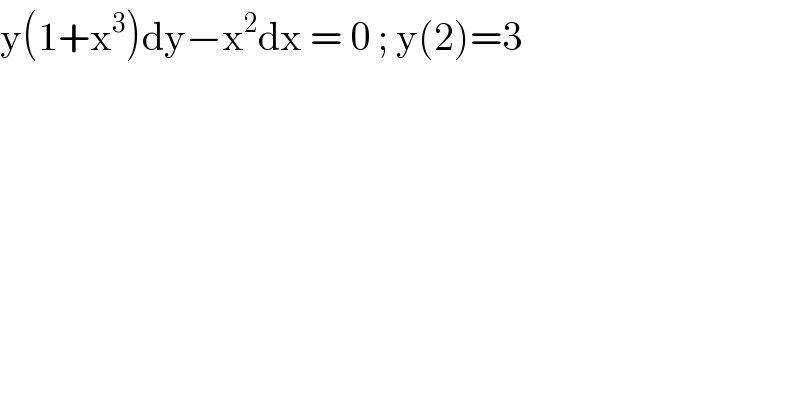
$$\mathrm{y}\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)\mathrm{dy}−\mathrm{x}^{\mathrm{2}} \mathrm{dx}\:=\:\mathrm{0}\:;\:\mathrm{y}\left(\mathrm{2}\right)=\mathrm{3}\: \\ $$
Answered by john santu last updated on 24/Jun/20
![y dy = ((x^2 dx)/(1+x^3 )) ⇒∫ y dy = (1/3)∫ ((d(x^3 +1))/(1+x^3 )) (1/2)[ y(x)]^2 = (1/3)ln(x^3 +1) +C [ y(x)]^2 = (2/3)ln(x^3 +1) + C_1 [ y(2)]^2 = (2/3)ln(9) + C_1 9 −(2/3)ln(9) = C_1 ∴ y^2 =(2/3)ln(x^3 +1)+9−(2/3)ln(9) y^2 = 9 + ln(((((x^3 +1)/9))^2 ))^(1/(3 )) ■](https://www.tinkutara.com/question/Q100016.png)
$$\mathrm{y}\:\mathrm{dy}\:=\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} } \\ $$$$\Rightarrow\int\:\mathrm{y}\:\mathrm{dy}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\:\mathrm{y}\left(\mathrm{x}\right)\right]^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\:+\mathrm{C}\: \\ $$$$\left[\:\mathrm{y}\left(\mathrm{x}\right)\right]\:^{\mathrm{2}} \:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\:+\:\mathrm{C}_{\mathrm{1}} \\ $$$$\left[\:\mathrm{y}\left(\mathrm{2}\right)\right]^{\mathrm{2}} \:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{9}\right)\:+\:\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{9}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{9}\right)\:=\:\mathrm{C}_{\mathrm{1}} \\ $$$$\therefore\:\mathrm{y}^{\mathrm{2}} \:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)+\mathrm{9}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{9}\right) \\ $$$$\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{9}\:+\:\mathrm{ln}\sqrt[{\mathrm{3}\:\:}]{\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{9}}\right)^{\mathrm{2}} }\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20
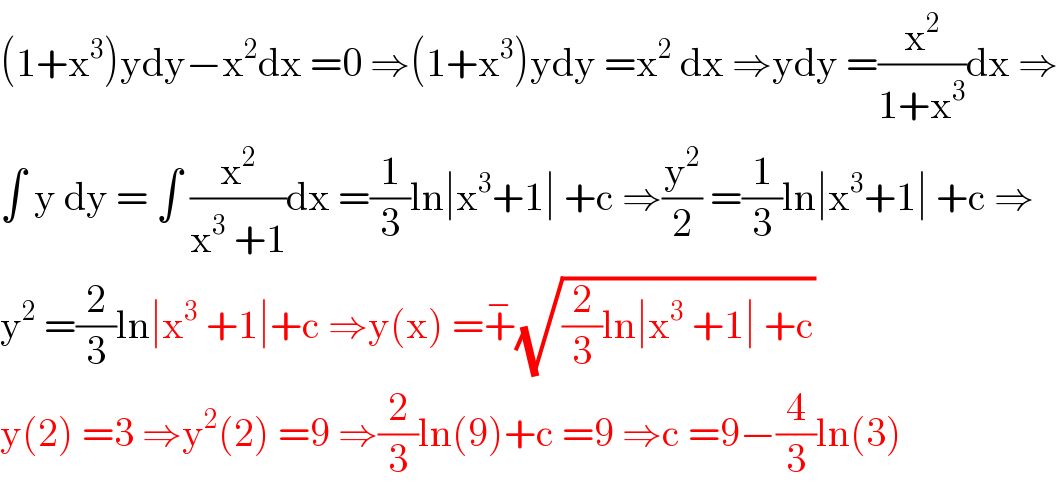
$$\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)\mathrm{ydy}−\mathrm{x}^{\mathrm{2}} \mathrm{dx}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)\mathrm{ydy}\:=\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}\:\Rightarrow\mathrm{ydy}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:\Rightarrow \\ $$$$\int\:\mathrm{y}\:\mathrm{dy}\:=\:\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{3}} +\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{3}} +\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}^{\mathrm{2}} \:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}\mid+\mathrm{c}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\overset{−} {+}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}\mid\:+\mathrm{c}} \\ $$$$\mathrm{y}\left(\mathrm{2}\right)\:=\mathrm{3}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \left(\mathrm{2}\right)\:=\mathrm{9}\:\Rightarrow\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{9}\right)+\mathrm{c}\:=\mathrm{9}\:\Rightarrow\mathrm{c}\:=\mathrm{9}−\frac{\mathrm{4}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{3}\right) \\ $$
