Question Number 155365 by MathsFan last updated on 29/Sep/21
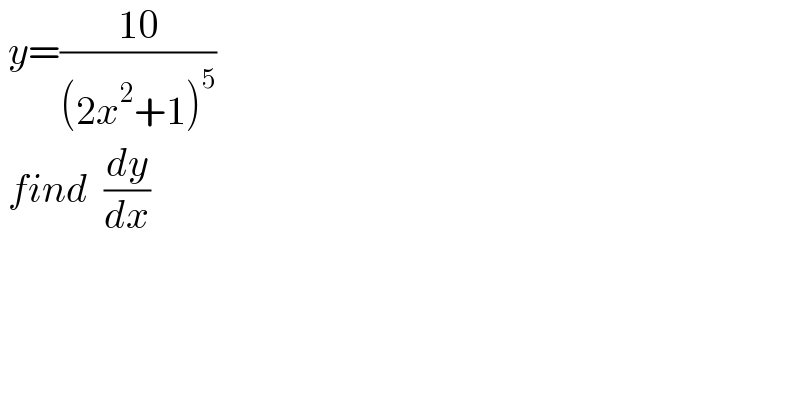
$$\:{y}=\frac{\mathrm{10}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} } \\ $$$$\:{find}\:\:\frac{{dy}}{{dx}} \\ $$
Answered by gsk2684 last updated on 29/Sep/21

$$\mathrm{10}\left(\frac{−\mathrm{5}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} }\right)\left(\mathrm{2}\left(\mathrm{2}{x}\right)+\mathrm{0}\right) \\ $$$$\frac{−\mathrm{200}{x}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} } \\ $$
Commented by MathsFan last updated on 29/Sep/21

$${correct}\:{sir} \\ $$
Answered by peter frank last updated on 29/Sep/21
![(dy/dx)=(((2x^2 +1)^5 (d/dx)(10)−10(d/dx)(2x^2 +1)^5 )/( [(2x^2 +1)^5 ]^2 )) (dy/dx)=((−10.5.(2x^2 +5)^4 .4x)/((2x^2 +1)^(10) )) (dy/dx)=((−200x)/((2x^2 +1)^6 ))](https://www.tinkutara.com/question/Q155375.png)
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\underline{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} \frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{10}\right)−\mathrm{10}\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} }}{\:\left[\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} \right]^{\mathrm{2}} } \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{−\mathrm{10}.\mathrm{5}.\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{4}} .\mathrm{4x}}{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{10}} } \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{−\mathrm{200x}}{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} } \\ $$
Commented by MathsFan last updated on 29/Sep/21

$${thank}\:{you} \\ $$
