Question Number 42291 by Joel578 last updated on 22/Aug/18
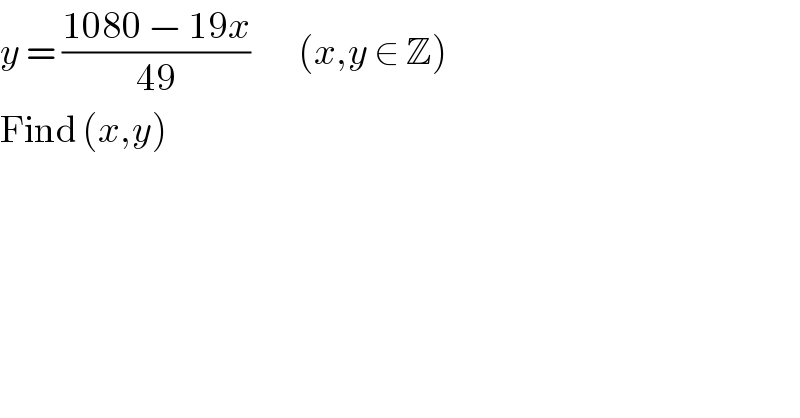
$${y}\:=\:\frac{\mathrm{1080}\:−\:\mathrm{19}{x}}{\mathrm{49}}\:\:\:\:\:\:\:\:\left({x},{y}\:\in\:\mathbb{Z}\right) \\ $$$$\mathrm{Find}\:\left({x},{y}\right) \\ $$
Answered by ajfour last updated on 22/Aug/18
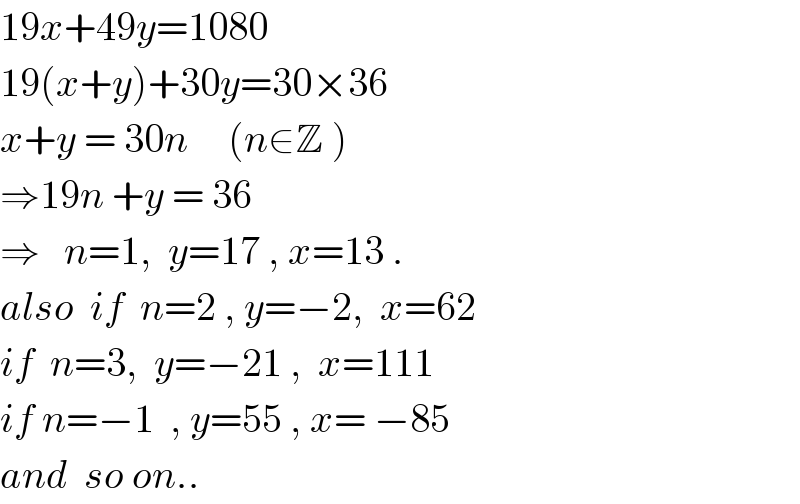
$$\mathrm{19}{x}+\mathrm{49}{y}=\mathrm{1080} \\ $$$$\mathrm{19}\left({x}+{y}\right)+\mathrm{30}{y}=\mathrm{30}×\mathrm{36} \\ $$$${x}+{y}\:=\:\mathrm{30}{n}\:\:\:\:\:\left({n}\in\mathbb{Z}\:\right) \\ $$$$\Rightarrow\mathrm{19}{n}\:+{y}\:=\:\mathrm{36} \\ $$$$\Rightarrow\:\:\:{n}=\mathrm{1},\:\:{y}=\mathrm{17}\:,\:{x}=\mathrm{13}\:. \\ $$$${also}\:\:{if}\:\:{n}=\mathrm{2}\:,\:{y}=−\mathrm{2},\:\:{x}=\mathrm{62} \\ $$$${if}\:\:{n}=\mathrm{3},\:\:{y}=−\mathrm{21}\:,\:\:{x}=\mathrm{111} \\ $$$${if}\:{n}=−\mathrm{1}\:\:,\:{y}=\mathrm{55}\:,\:{x}=\:−\mathrm{85} \\ $$$${and}\:\:{so}\:{on}.. \\ $$
Commented by Joel578 last updated on 22/Aug/18
$${thank}\:{you}\:{very}\:{much} \\ $$
