Question Number 127505 by bramlexs22 last updated on 30/Dec/20
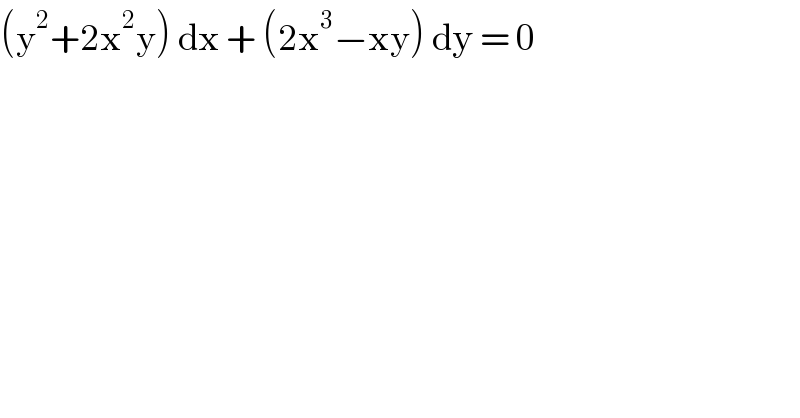
$$\left(\mathrm{y}^{\mathrm{2}} +\mathrm{2x}^{\mathrm{2}} \mathrm{y}\right)\:\mathrm{dx}\:+\:\left(\mathrm{2x}^{\mathrm{3}} −\mathrm{xy}\right)\:\mathrm{dy}\:=\:\mathrm{0} \\ $$
Answered by liberty last updated on 30/Dec/20
![(dy/dx) = ((y^2 +2x^2 y)/(xy−2x^3 )) ; let y = vx^2 ⇒(dy/dx) = 2vx + x^2 (dv/dx) we find 2vx+x^2 (dv/dx) = ((x^4 (v^2 +2v))/(x^3 (v−2))) 2vx + x^2 (dv/dx) = ((x(v^2 +2v))/(v−2)) 2v+x (dv/dx) = ((v^2 +2v)/(v−2)) ; x (dv/dx) = ((v^2 +2v−2v^2 +4v)/(v−2)) ((v−2)/(v^2 −6v)) dv + (dx/x) = 0 _; [ ((v−2)/(v(v−6))) =(Q/v)+(R/(v−6))] ∫[ (1/(3v)) +(2/(3(v−6)))] dv + ∫ (dx/x) = C (1/3)(ln v+ln (v−6)^2 )+ln x = C ln ((v−6)^2 v) = ln ((C_1 /x))^3 (((y−6x^2 )/x^2 ))^2 ((y/x^2 )) = (λ/x^4 ) ⇒ y(y−6x^2 )^2 =λx^2](https://www.tinkutara.com/question/Q127507.png)
$$\:\frac{{dy}}{{dx}}\:=\:\frac{{y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} {y}}{{xy}−\mathrm{2}{x}^{\mathrm{3}} }\:;\:{let}\:{y}\:=\:{vx}^{\mathrm{2}} \:\Rightarrow\frac{{dy}}{{dx}}\:=\:\mathrm{2}{vx}\:+\:{x}^{\mathrm{2}} \:\frac{{dv}}{{dx}} \\ $$$${we}\:{find}\:\mathrm{2}{vx}+{x}^{\mathrm{2}} \:\frac{{dv}}{{dx}}\:=\:\frac{{x}^{\mathrm{4}} \left({v}^{\mathrm{2}} +\mathrm{2}{v}\right)}{{x}^{\mathrm{3}} \left({v}−\mathrm{2}\right)} \\ $$$$\:\mathrm{2}{vx}\:+\:{x}^{\mathrm{2}} \:\frac{{dv}}{{dx}}\:=\:\frac{{x}\left({v}^{\mathrm{2}} +\mathrm{2}{v}\right)}{{v}−\mathrm{2}} \\ $$$$\:\:\mathrm{2}{v}+{x}\:\frac{{dv}}{{dx}}\:=\:\frac{{v}^{\mathrm{2}} +\mathrm{2}{v}}{{v}−\mathrm{2}}\:;\:{x}\:\frac{{dv}}{{dx}}\:=\:\frac{{v}^{\mathrm{2}} +\mathrm{2}{v}−\mathrm{2}{v}^{\mathrm{2}} +\mathrm{4}{v}}{{v}−\mathrm{2}} \\ $$$$\:\frac{{v}−\mathrm{2}}{{v}^{\mathrm{2}} −\mathrm{6}{v}}\:{dv}\:+\:\frac{{dx}}{{x}}\:=\:\mathrm{0}\:\:\_;\:\left[\:\frac{{v}−\mathrm{2}}{{v}\left({v}−\mathrm{6}\right)}\:=\frac{{Q}}{{v}}+\frac{{R}}{{v}−\mathrm{6}}\right]\: \\ $$$$\:\int\left[\:\frac{\mathrm{1}}{\mathrm{3}{v}}\:+\frac{\mathrm{2}}{\mathrm{3}\left({v}−\mathrm{6}\right)}\right]\:{dv}\:+\:\int\:\frac{{dx}}{{x}}\:=\:{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln}\:{v}+\mathrm{ln}\:\left({v}−\mathrm{6}\right)^{\mathrm{2}} \right)+\mathrm{ln}\:{x}\:=\:{C} \\ $$$$\:\mathrm{ln}\:\left(\left({v}−\mathrm{6}\right)^{\mathrm{2}} {v}\right)\:=\:\mathrm{ln}\:\left(\frac{{C}_{\mathrm{1}} }{{x}}\right)^{\mathrm{3}} \\ $$$$\:\:\:\left(\frac{{y}−\mathrm{6}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(\frac{{y}}{{x}^{\mathrm{2}} }\right)\:=\:\frac{\lambda}{{x}^{\mathrm{4}} }\:\Rightarrow\:{y}\left({y}−\mathrm{6}{x}^{\mathrm{2}} \right)^{\mathrm{2}} =\lambda{x}^{\mathrm{2}} \: \\ $$$$ \\ $$
