Question Number 96713 by Tony Lin last updated on 04/Jun/20

$${y}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{dy}}{{dx}} \\ $$
Answered by mr W last updated on 04/Jun/20
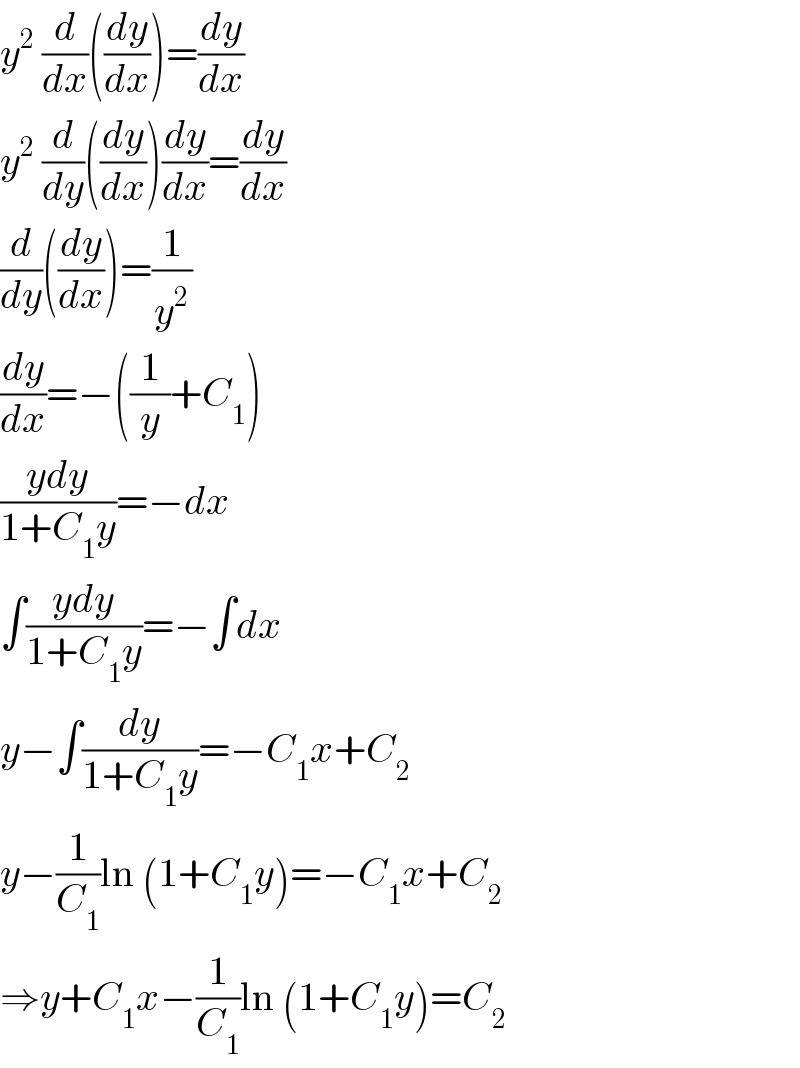
$${y}^{\mathrm{2}} \:\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{dy}}{{dx}} \\ $$$${y}^{\mathrm{2}} \:\frac{{d}}{{dy}}\left(\frac{{dy}}{{dx}}\right)\frac{{dy}}{{dx}}=\frac{{dy}}{{dx}} \\ $$$$\frac{{d}}{{dy}}\left(\frac{{dy}}{{dx}}\right)=\frac{\mathrm{1}}{{y}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=−\left(\frac{\mathrm{1}}{{y}}+{C}_{\mathrm{1}} \right) \\ $$$$\frac{{ydy}}{\mathrm{1}+{C}_{\mathrm{1}} {y}}=−{dx} \\ $$$$\int\frac{{ydy}}{\mathrm{1}+{C}_{\mathrm{1}} {y}}=−\int{dx} \\ $$$${y}−\int\frac{{dy}}{\mathrm{1}+{C}_{\mathrm{1}} {y}}=−{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$${y}−\frac{\mathrm{1}}{{C}_{\mathrm{1}} }\mathrm{ln}\:\left(\mathrm{1}+{C}_{\mathrm{1}} {y}\right)=−{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{y}+{C}_{\mathrm{1}} {x}−\frac{\mathrm{1}}{{C}_{\mathrm{1}} }\mathrm{ln}\:\left(\mathrm{1}+{C}_{\mathrm{1}} {y}\right)={C}_{\mathrm{2}} \\ $$
Commented by Tony Lin last updated on 04/Jun/20

$${thanks}\:{sir} \\ $$
