Question Number 103483 by bemath last updated on 15/Jul/20
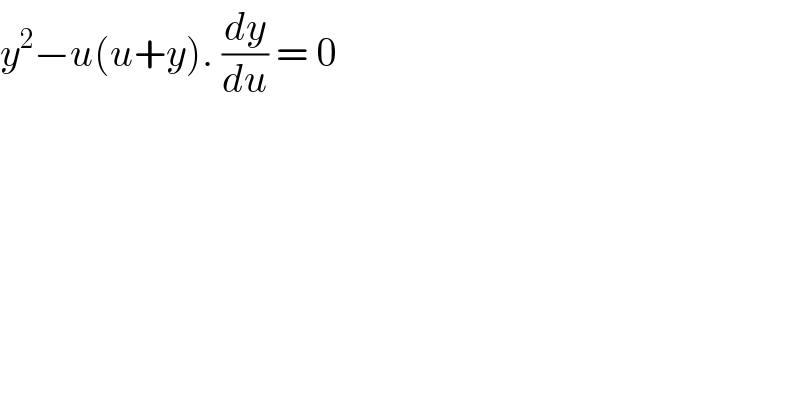
$${y}^{\mathrm{2}} −{u}\left({u}+{y}\right).\:\frac{{dy}}{{du}}\:=\:\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jul/20
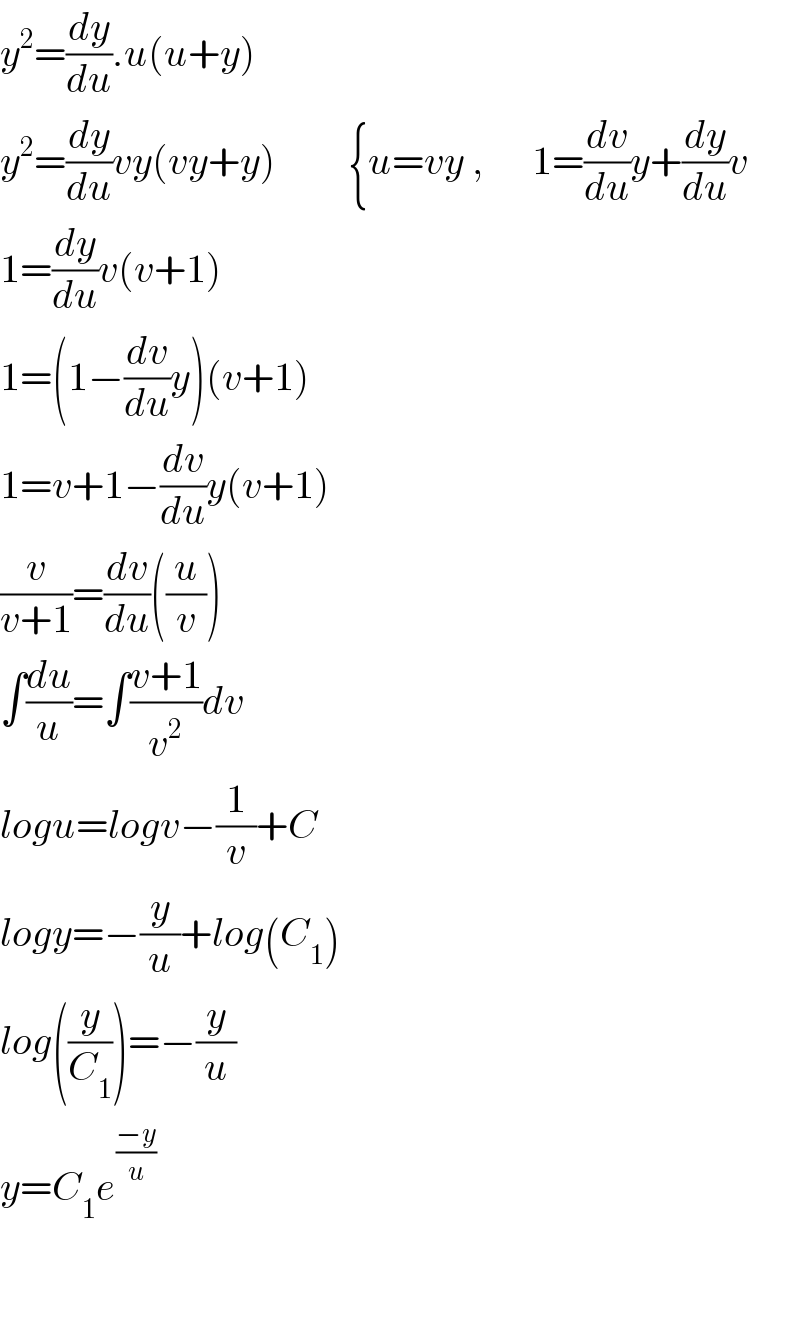
$${y}^{\mathrm{2}} =\frac{{dy}}{{du}}.{u}\left({u}+{y}\right) \\ $$$${y}^{\mathrm{2}} =\frac{{dy}}{{du}}{vy}\left({vy}+{y}\right)\:\:\:\:\:\:\:\:\:\left\{{u}={vy}\:,\:\:\:\:\:\:\mathrm{1}=\frac{{dv}}{{du}}{y}+\frac{{dy}}{{du}}{v}\right. \\ $$$$\mathrm{1}=\frac{{dy}}{{du}}{v}\left({v}+\mathrm{1}\right) \\ $$$$\mathrm{1}=\left(\mathrm{1}−\frac{{dv}}{{du}}{y}\right)\left({v}+\mathrm{1}\right) \\ $$$$\mathrm{1}={v}+\mathrm{1}−\frac{{dv}}{{du}}{y}\left({v}+\mathrm{1}\right) \\ $$$$\frac{{v}}{{v}+\mathrm{1}}=\frac{{dv}}{{du}}\left(\frac{{u}}{{v}}\right) \\ $$$$\int\frac{{du}}{{u}}=\int\frac{{v}+\mathrm{1}}{{v}^{\mathrm{2}} }{dv} \\ $$$${logu}={logv}−\frac{\mathrm{1}}{{v}}+{C} \\ $$$${logy}=−\frac{{y}}{{u}}+{log}\left({C}_{\mathrm{1}} \right) \\ $$$${log}\left(\frac{{y}}{{C}_{\mathrm{1}} }\right)=−\frac{{y}}{{u}} \\ $$$${y}={C}_{\mathrm{1}} {e}^{\frac{−{y}}{{u}}} \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 15/Jul/20
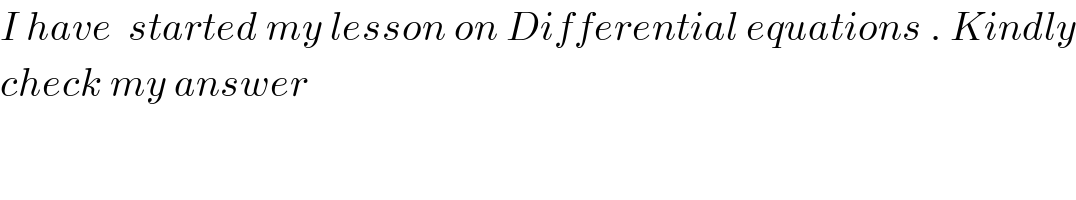
$${I}\:{have}\:\:{started}\:{my}\:{lesson}\:{on}\:{Differential}\:{equations}\:.\:{Kindly} \\ $$$${check}\:{my}\:{answer} \\ $$
Answered by bramlex last updated on 15/Jul/20
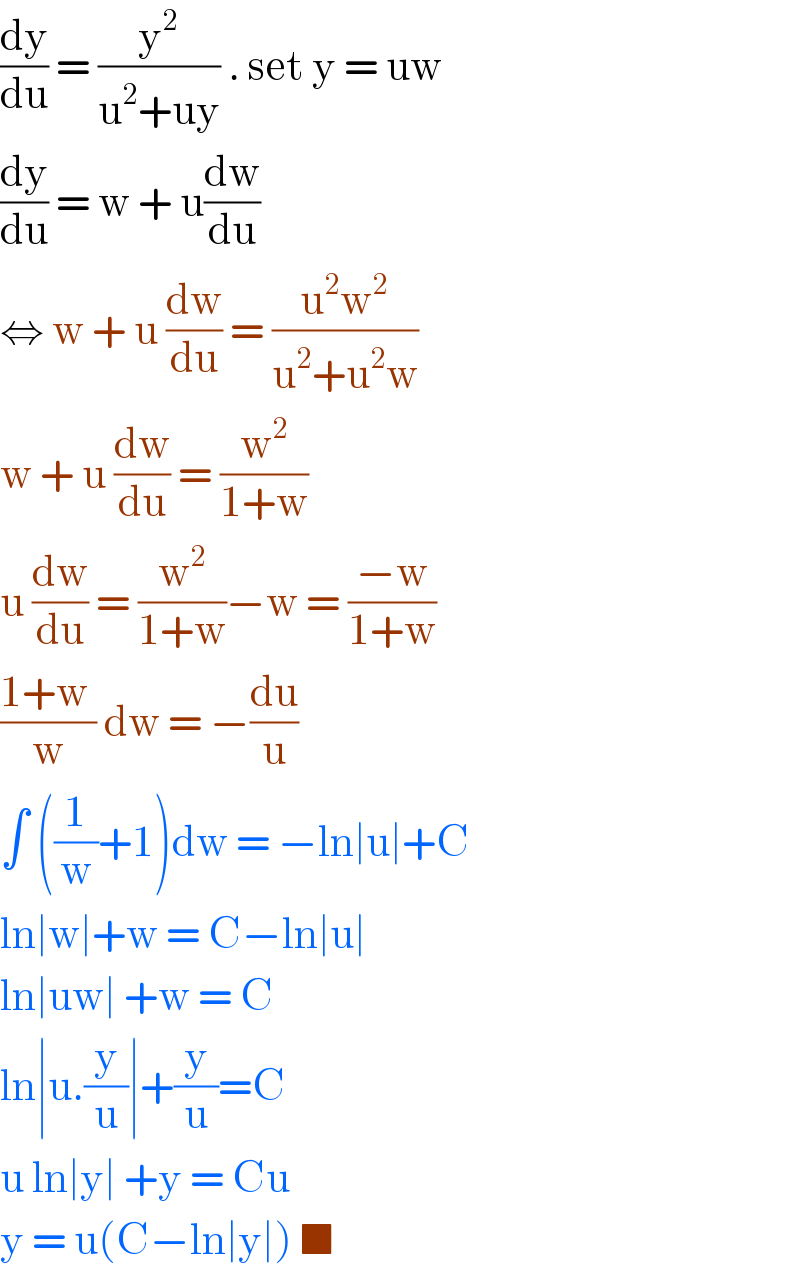
$$\frac{\mathrm{dy}}{\mathrm{du}}\:=\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} +\mathrm{uy}}\:.\:\mathrm{set}\:\mathrm{y}\:=\:\mathrm{uw}\: \\ $$$$\frac{\mathrm{dy}}{\mathrm{du}}\:=\:\mathrm{w}\:+\:\mathrm{u}\frac{\mathrm{dw}}{\mathrm{du}} \\ $$$$\Leftrightarrow\:\mathrm{w}\:+\:\mathrm{u}\:\frac{\mathrm{dw}}{\mathrm{du}}\:=\:\frac{\mathrm{u}^{\mathrm{2}} \mathrm{w}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \mathrm{w}} \\ $$$$\mathrm{w}\:+\:\mathrm{u}\:\frac{\mathrm{dw}}{\mathrm{du}}\:=\:\frac{\mathrm{w}^{\mathrm{2}} }{\mathrm{1}+\mathrm{w}} \\ $$$$\mathrm{u}\:\frac{\mathrm{dw}}{\mathrm{du}}\:=\:\frac{\mathrm{w}^{\mathrm{2}} }{\mathrm{1}+\mathrm{w}}−\mathrm{w}\:=\:\frac{−\mathrm{w}}{\mathrm{1}+\mathrm{w}} \\ $$$$\frac{\mathrm{1}+\mathrm{w}\:}{\mathrm{w}}\:\mathrm{dw}\:=\:−\frac{\mathrm{du}}{\mathrm{u}}\: \\ $$$$\int\:\left(\frac{\mathrm{1}}{\mathrm{w}}+\mathrm{1}\right)\mathrm{dw}\:=\:−\mathrm{ln}\mid\mathrm{u}\mid+\mathrm{C} \\ $$$$\mathrm{ln}\mid\mathrm{w}\mid+\mathrm{w}\:=\:\mathrm{C}−\mathrm{ln}\mid\mathrm{u}\mid \\ $$$$\mathrm{ln}\mid\mathrm{uw}\mid\:+\mathrm{w}\:=\:\mathrm{C} \\ $$$$\mathrm{ln}\mid\mathrm{u}.\frac{\mathrm{y}}{\mathrm{u}}\mid+\frac{\mathrm{y}}{\mathrm{u}}=\mathrm{C} \\ $$$$\mathrm{u}\:\mathrm{ln}\mid\mathrm{y}\mid\:+\mathrm{y}\:=\:\mathrm{Cu} \\ $$$$\mathrm{y}\:=\:\mathrm{u}\left(\mathrm{C}−\mathrm{ln}\mid\mathrm{y}\mid\right)\:\blacksquare\: \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
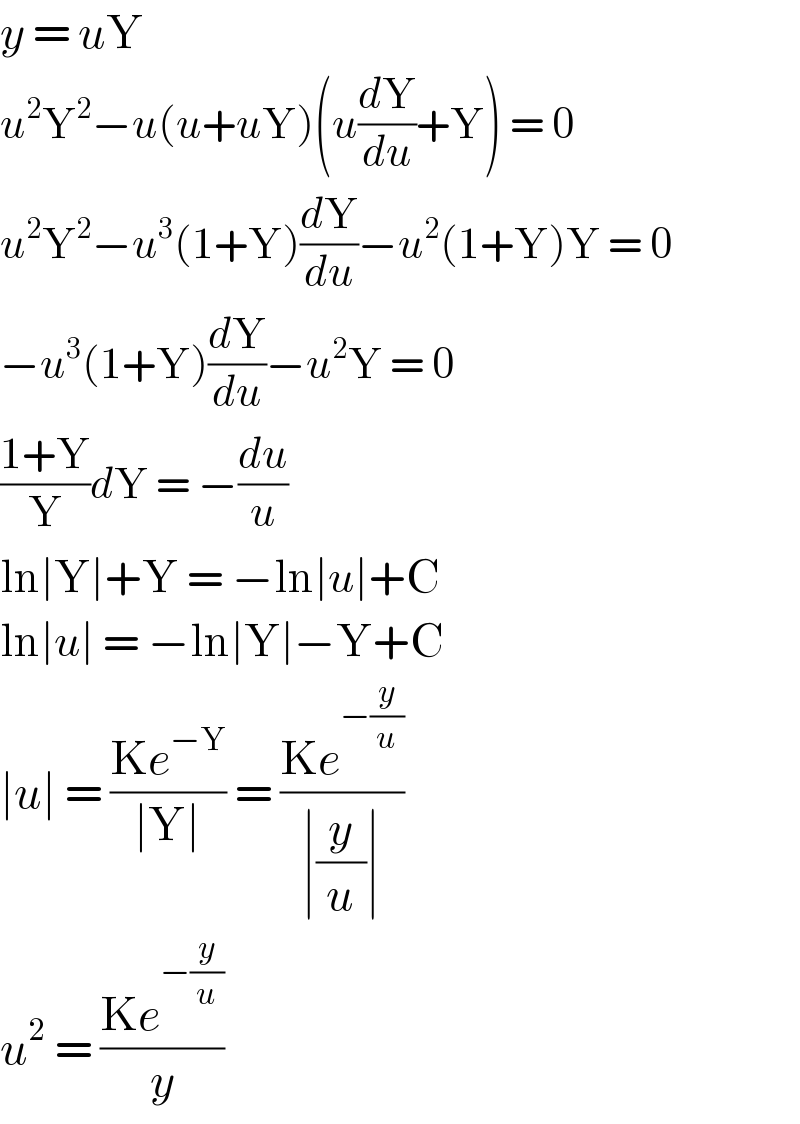
$${y}\:=\:{u}\mathrm{Y} \\ $$$${u}^{\mathrm{2}} \mathrm{Y}^{\mathrm{2}} −{u}\left({u}+{u}\mathrm{Y}\right)\left({u}\frac{{d}\mathrm{Y}}{{du}}+\mathrm{Y}\right)\:=\:\mathrm{0} \\ $$$${u}^{\mathrm{2}} \mathrm{Y}^{\mathrm{2}} −{u}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{Y}\right)\frac{{d}\mathrm{Y}}{{du}}−{u}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{Y}\right)\mathrm{Y}\:=\:\mathrm{0} \\ $$$$−{u}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{Y}\right)\frac{{d}\mathrm{Y}}{{du}}−{u}^{\mathrm{2}} \mathrm{Y}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}+\mathrm{Y}}{\mathrm{Y}}{d}\mathrm{Y}\:=\:−\frac{{du}}{{u}} \\ $$$$\mathrm{ln}\mid\mathrm{Y}\mid+\mathrm{Y}\:=\:−\mathrm{ln}\mid{u}\mid+\mathrm{C} \\ $$$$\mathrm{ln}\mid{u}\mid\:=\:−\mathrm{ln}\mid\mathrm{Y}\mid−\mathrm{Y}+\mathrm{C} \\ $$$$\mid{u}\mid\:=\:\frac{\mathrm{K}{e}^{−\mathrm{Y}} }{\mid\mathrm{Y}\mid}\:=\:\frac{\mathrm{K}{e}^{−\frac{{y}}{{u}}} }{\mid\frac{{y}}{{u}}\mid} \\ $$$${u}^{\mathrm{2}} \:=\:\frac{\mathrm{K}{e}^{−\frac{{y}}{{u}}} }{{y}} \\ $$
