y-2-y-

Question Number 87905 by john santu last updated on 07/Apr/20

$$\mathrm{y}'\:=\:\mathrm{2}^{\mathrm{y}} \\ $$

Commented by john santu last updated on 07/Apr/20

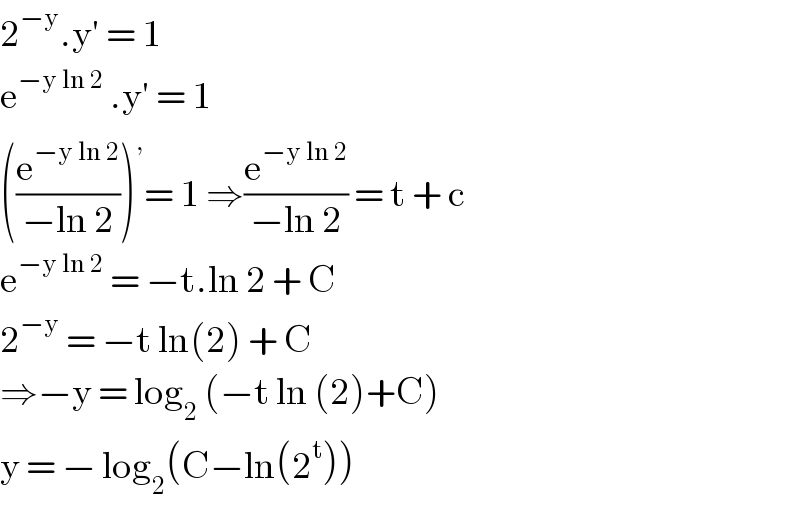
2^(−y) .y′ = 1 e^(−y ln 2) .y′ = 1 ((e^(−y ln 2) /(−ln 2)))^, = 1 ⇒(e^(−y ln 2) /(−ln 2)) = t + c e^(−y ln 2) = −t.ln 2 + C 2^(−y) = −t ln(2) + C ⇒−y = log_2 (−t ln (2)+C) y = − log_2 (C−ln(2^t ))

$$\mathrm{2}^{−\mathrm{y}} .\mathrm{y}'\:=\:\mathrm{1} \\ $$$$\mathrm{e}^{−\mathrm{y}\:\mathrm{ln}\:\mathrm{2}} \:.\mathrm{y}'\:=\:\mathrm{1}\: \\ $$$$\left(\frac{\mathrm{e}^{−\mathrm{y}\:\mathrm{ln}\:\mathrm{2}} }{−\mathrm{ln}\:\mathrm{2}}\right)^{,} =\:\mathrm{1}\:\Rightarrow\frac{\mathrm{e}^{−\mathrm{y}\:\mathrm{ln}\:\mathrm{2}} }{−\mathrm{ln}\:\mathrm{2}}\:=\:\mathrm{t}\:+\:\mathrm{c} \\ $$$$\mathrm{e}^{−\mathrm{y}\:\mathrm{ln}\:\mathrm{2}} \:=\:−\mathrm{t}.\mathrm{ln}\:\mathrm{2}\:+\:\mathrm{C} \\ $$$$\mathrm{2}^{−\mathrm{y}} \:=\:−\mathrm{t}\:\mathrm{ln}\left(\mathrm{2}\right)\:+\:\mathrm{C} \\ $$$$\Rightarrow−\mathrm{y}\:=\:\mathrm{log}_{\mathrm{2}} \:\left(−\mathrm{t}\:\mathrm{ln}\:\left(\mathrm{2}\right)+\mathrm{C}\right) \\ $$$$\mathrm{y}\:=\:−\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{C}−\mathrm{ln}\left(\mathrm{2}^{\mathrm{t}} \right)\right) \\ $$

Answered by Joel578 last updated on 07/Apr/20

(dy/dx) = 2^y ⇒ ∫ 2^(−y) dy = ∫ dx ⇒ −(2^(−y) /(ln 2)) = x + C_1 ⇒ 2^(−y) = (C_2 − x)ln 2 , C_2 = −C_1 ⇒ −y ln 2 = ln [(C_2 − x)ln 2] ⇒ y(x) = −((ln [(C_2 − x)ln 2])/(ln 2)) = − log_2 [(C_2 − x)ln 2]

$$\frac{{dy}}{{dx}}\:=\:\mathrm{2}^{{y}} \:\Rightarrow\:\int\:\mathrm{2}^{−{y}} \:{dy}\:=\:\int\:{dx} \\ $$$$\Rightarrow\:−\frac{\mathrm{2}^{−{y}} }{\mathrm{ln}\:\mathrm{2}}\:=\:{x}\:+\:{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{2}^{−{y}} \:=\:\left({C}_{\mathrm{2}} \:−\:{x}\right)\mathrm{ln}\:\mathrm{2}\:\:\:\:\:,\:\:{C}_{\mathrm{2}} \:=\:−{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:−{y}\:\mathrm{ln}\:\mathrm{2}\:=\:\mathrm{ln}\:\left[\left({C}_{\mathrm{2}} \:−\:{x}\right)\mathrm{ln}\:\mathrm{2}\right]\: \\ $$$$\Rightarrow\:{y}\left({x}\right)\:=\:−\frac{\mathrm{ln}\:\left[\left({C}_{\mathrm{2}} \:−\:{x}\right)\mathrm{ln}\:\mathrm{2}\right]}{\mathrm{ln}\:\mathrm{2}}\:=\:−\:\mathrm{log}_{\mathrm{2}} \:\left[\left({C}_{\mathrm{2}} \:−\:{x}\right)\mathrm{ln}\:\mathrm{2}\right] \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply