Question Number 26904 by sorour87 last updated on 31/Dec/17

$${y}^{\left(\mathrm{2}\right)} +{y}=\mathrm{sec}\:^{\mathrm{3}} {x} \\ $$
Commented by prakash jain last updated on 31/Dec/17
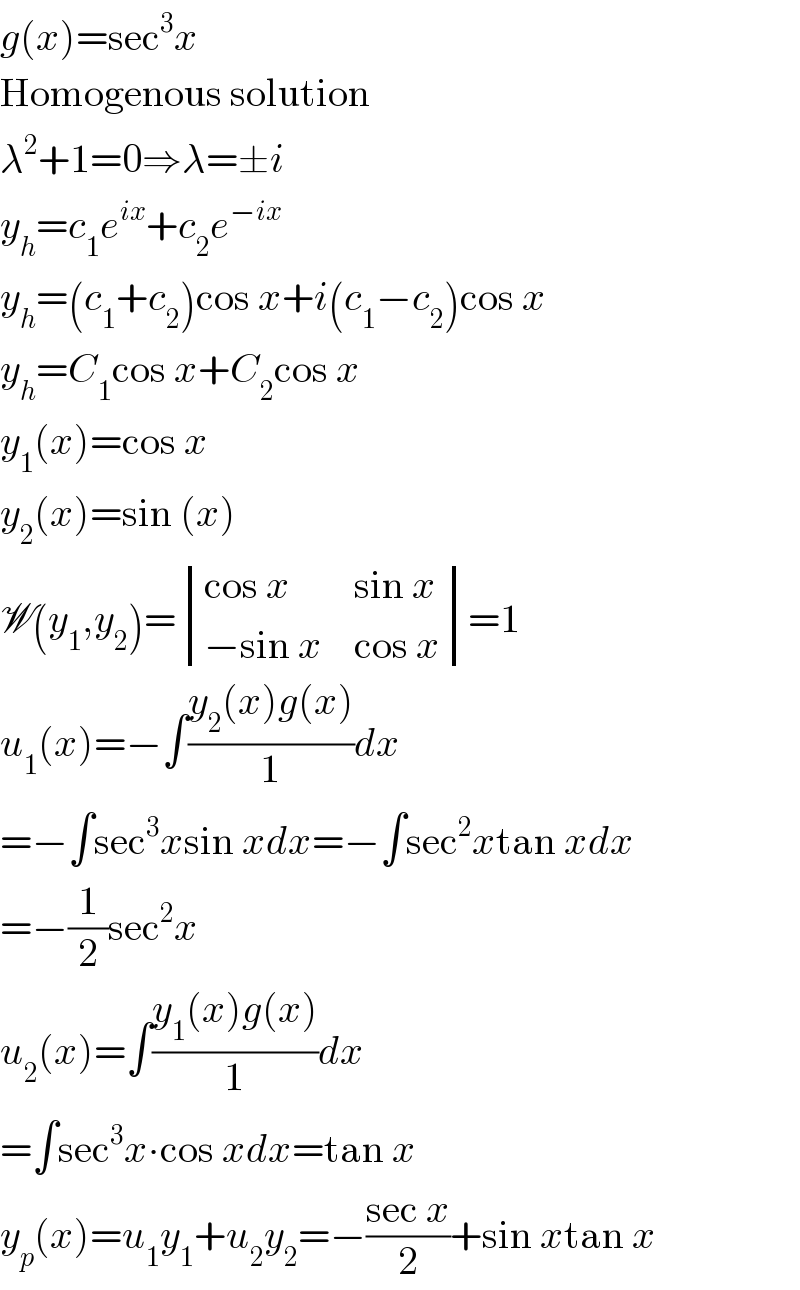
$${g}\left({x}\right)=\mathrm{sec}^{\mathrm{3}} {x} \\ $$$$\mathrm{Homogenous}\:\mathrm{solution} \\ $$$$\lambda^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow\lambda=\pm{i} \\ $$$${y}_{{h}} ={c}_{\mathrm{1}} {e}^{{ix}} +{c}_{\mathrm{2}} {e}^{−{ix}} \\ $$$${y}_{{h}} =\left({c}_{\mathrm{1}} +{c}_{\mathrm{2}} \right)\mathrm{cos}\:{x}+{i}\left({c}_{\mathrm{1}} −{c}_{\mathrm{2}} \right)\mathrm{cos}\:{x} \\ $$$${y}_{{h}} ={C}_{\mathrm{1}} \mathrm{cos}\:{x}+{C}_{\mathrm{2}} \mathrm{cos}\:{x} \\ $$$${y}_{\mathrm{1}} \left({x}\right)=\mathrm{cos}\:{x} \\ $$$${y}_{\mathrm{2}} \left({x}\right)=\mathrm{sin}\:\left({x}\right) \\ $$$$\mathscr{W}\left({y}_{\mathrm{1}} ,{y}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{cos}\:{x}}&{\mathrm{sin}\:{x}}\\{−\mathrm{sin}\:{x}}&{\mathrm{cos}\:{x}}\end{vmatrix}=\mathrm{1} \\ $$$${u}_{\mathrm{1}} \left({x}\right)=−\int\frac{{y}_{\mathrm{2}} \left({x}\right){g}\left({x}\right)}{\mathrm{1}}{dx} \\ $$$$=−\int\mathrm{sec}^{\mathrm{3}} {x}\mathrm{sin}\:{xdx}=−\int\mathrm{sec}^{\mathrm{2}} {x}\mathrm{tan}\:{xdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} {x} \\ $$$${u}_{\mathrm{2}} \left({x}\right)=\int\frac{{y}_{\mathrm{1}} \left({x}\right){g}\left({x}\right)}{\mathrm{1}}{dx} \\ $$$$=\int\mathrm{sec}^{\mathrm{3}} {x}\centerdot\mathrm{cos}\:{xdx}=\mathrm{tan}\:{x} \\ $$$${y}_{{p}} \left({x}\right)={u}_{\mathrm{1}} {y}_{\mathrm{1}} +{u}_{\mathrm{2}} {y}_{\mathrm{2}} =−\frac{\mathrm{sec}\:{x}}{\mathrm{2}}+\mathrm{sin}\:{x}\mathrm{tan}\:{x} \\ $$
Answered by prakash jain last updated on 31/Dec/17

$${y}={y}_{{h}} +{y}_{{p}} \\ $$
Commented by sorour87 last updated on 31/Dec/17

$${ok}.\:{thanks} \\ $$
Commented by prakash jain last updated on 31/Dec/17
The following page desxribes the method of variation of parameters.
http://tutorial.math.lamar.edu/Classes/DE/VariationofParameters.aspx
