Question Number 84212 by jagoll last updated on 10/Mar/20
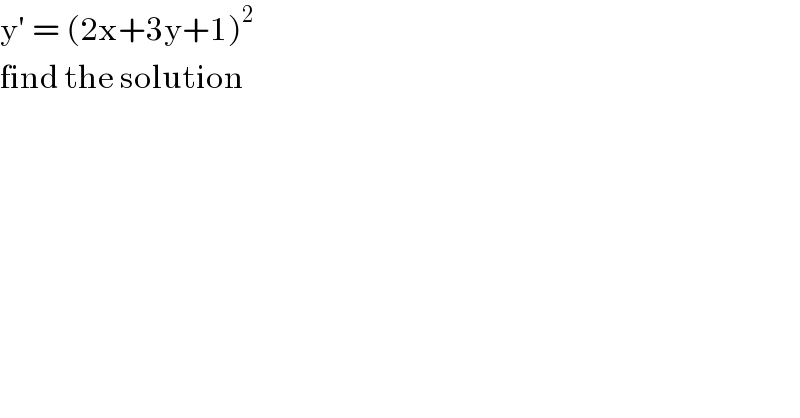
$$\mathrm{y}'\:=\:\left(\mathrm{2x}+\mathrm{3y}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\: \\ $$
Commented by niroj last updated on 10/Mar/20

$$\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\left(\mathrm{2x}+\mathrm{3y}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{put},\:\:\mathrm{2x}+\mathrm{3y}+\mathrm{1}=\mathrm{v} \\ $$$$\:\:\:\:\:\mathrm{2}+\mathrm{3}\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{2}\right) \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{2}\right)=\mathrm{v}^{\mathrm{2}} \\ $$$$\:\:\:\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{2}=\mathrm{3v}^{\mathrm{2}} \\ $$$$\:\:\:\:\frac{\mathrm{dv}}{\mathrm{dx}}=\:\mathrm{3v}^{\mathrm{2}} +\mathrm{2} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{3v}^{\mathrm{2}} +\mathrm{2}}\mathrm{dv}=\mathrm{dx} \\ $$$$\:\:\:\mathrm{integrating}\:\mathrm{both}\:\mathrm{side}. \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\frac{\mathrm{1}}{\left(\mathrm{v}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\right)^{\mathrm{2}} }\mathrm{dv}=\int\mathrm{dx} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{v}}{\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}}\:=\:\mathrm{x}+\mathrm{c} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}.\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{v}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\:=\mathrm{x}+\mathrm{c} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \:\mathrm{v}\:\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}=\mathrm{x}+\mathrm{c} \\ $$$$\:\:\:\:\mathrm{tan}^{−\mathrm{1}} \mathrm{v}.\:\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}=\:\sqrt{\mathrm{6}}\:\left(\mathrm{x}+\mathrm{c}\right) \\ $$$$\:\:\:\:\:\:\frac{\mathrm{v}\sqrt{\mathrm{6}}}{\mathrm{2}}=\:\mathrm{tan}\sqrt{\mathrm{6}}\:\:\left(\mathrm{x}+\mathrm{c}\right) \\ $$$$\:\:\:\:\:\:\left(\mathrm{2x}+\mathrm{3y}+\mathrm{1}\right)\sqrt{\mathrm{6}}\:=\mathrm{2}\:\mathrm{tan}\sqrt{\mathrm{6}}\:\left(\mathrm{x}+\mathrm{c}\right) \\ $$$$\:\:\mathrm{2x}+\mathrm{3y}+\mathrm{1}\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\:\mathrm{tan}\sqrt{\mathrm{6}}\:\:\left(\mathrm{x}+\mathrm{c}\right)\:. \\ $$$$\: \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 10/Mar/20
![let t=2x+3y+1 (dt/dx)=2+3(dy/dx) y′=(dy/dx)=(1/3)((dt/dx)−2) (1/3)((dt/dx)−2)=t^2 (dt/dx)=3t^2 +2 (dt/(3t^2 +2))=dx ∫(dt/(3t^2 +2))=∫dx ((tan^(−1) ((3t)/( (√6))))/( (√6)))=x+C ⇒t=((√6)/3) tan ((√6)x+C) ⇒2x+3y+1=((√6)/3) tan ((√6)x+C) ⇒y=(1/3)[((√6)/3) tan ((√6)x+C)−2x−1]](https://www.tinkutara.com/question/Q84214.png)
$${let}\:{t}=\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{1} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{2}+\mathrm{3}\frac{{dy}}{{dx}} \\ $$$${y}'=\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{dt}}{{dx}}−\mathrm{2}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{dt}}{{dx}}−\mathrm{2}\right)={t}^{\mathrm{2}} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2} \\ $$$$\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}}={dx} \\ $$$$\int\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}}=\int{dx} \\ $$$$\frac{\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}{t}}{\:\sqrt{\mathrm{6}}}}{\:\sqrt{\mathrm{6}}}={x}+{C} \\ $$$$\Rightarrow{t}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{6}}{x}+{C}\right) \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{1}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{6}}{x}+{C}\right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{6}}{x}+{C}\right)−\mathrm{2}{x}−\mathrm{1}\right] \\ $$
