Question Number 93059 by Ar Brandon last updated on 10/May/20
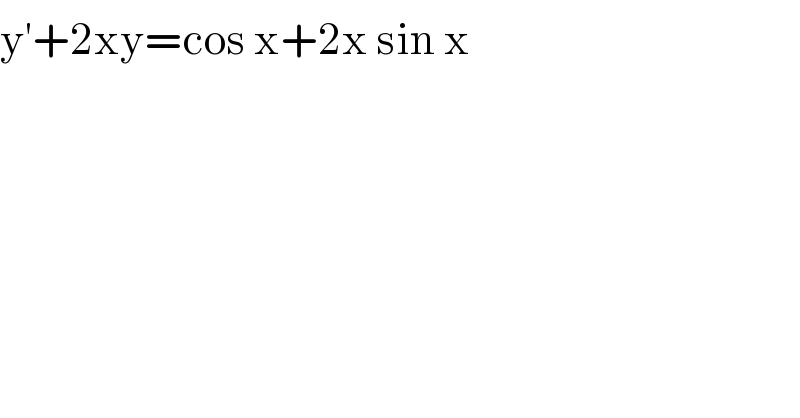
$$\mathrm{y}^{'} +\mathrm{2xy}=\mathrm{cos}\:\mathrm{x}+\mathrm{2x}\:\mathrm{sin}\:\mathrm{x} \\ $$
Answered by TANMAY PANACEA … last updated on 10/May/20
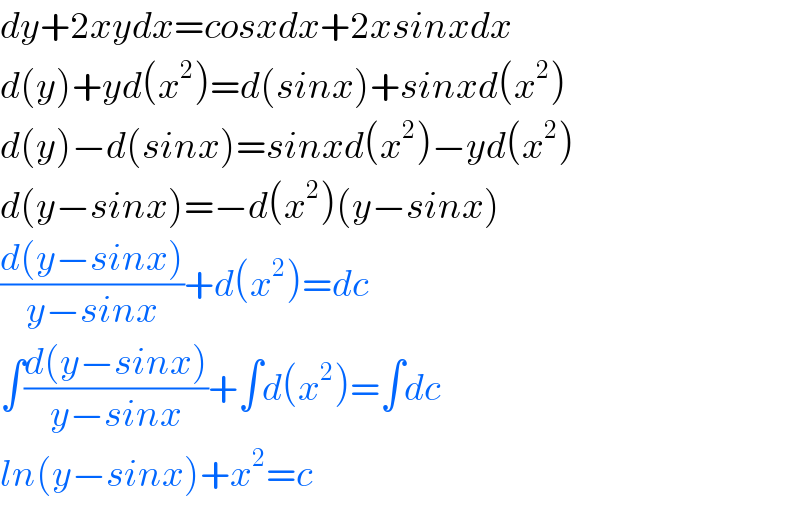
$${dy}+\mathrm{2}{xydx}={cosxdx}+\mathrm{2}{xsinxdx} \\ $$$${d}\left({y}\right)+{yd}\left({x}^{\mathrm{2}} \right)={d}\left({sinx}\right)+{sinxd}\left({x}^{\mathrm{2}} \right) \\ $$$${d}\left({y}\right)−{d}\left({sinx}\right)={sinxd}\left({x}^{\mathrm{2}} \right)−{yd}\left({x}^{\mathrm{2}} \right) \\ $$$${d}\left({y}−{sinx}\right)=−{d}\left({x}^{\mathrm{2}} \right)\left({y}−{sinx}\right) \\ $$$$\frac{{d}\left({y}−{sinx}\right)}{{y}−{sinx}}+{d}\left({x}^{\mathrm{2}} \right)={dc} \\ $$$$\int\frac{{d}\left({y}−{sinx}\right)}{{y}−{sinx}}+\int{d}\left({x}^{\mathrm{2}} \right)=\int{dc} \\ $$$${ln}\left({y}−{sinx}\right)+{x}^{\mathrm{2}} ={c} \\ $$
Commented by Ar Brandon last updated on 10/May/20
Thanks ��
