Menu Close

y-2y-3y-e-x-e-2x-

Tinku Tara 0 Comments
Pin




Question Number 92702 by i jagooll last updated on 08/May/20
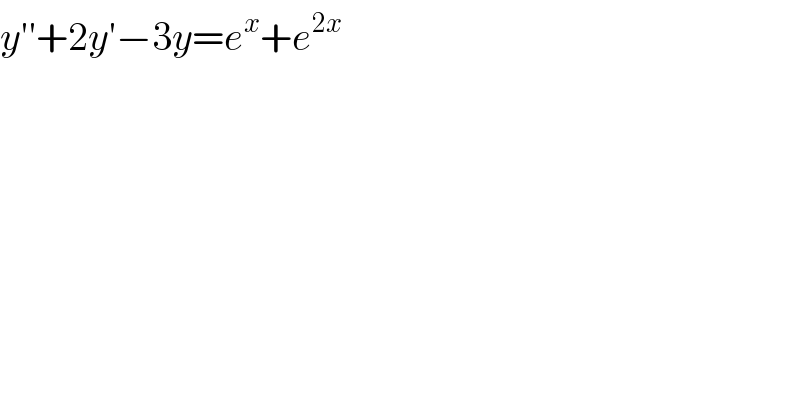
y′′+2y′−3y=e^x +e^(2x)
$${y}''+\mathrm{2}{y}'−\mathrm{3}{y}={e}^{{x}} +{e}^{\mathrm{2}{x}} \\ $$
Answered by niroj last updated on 08/May/20
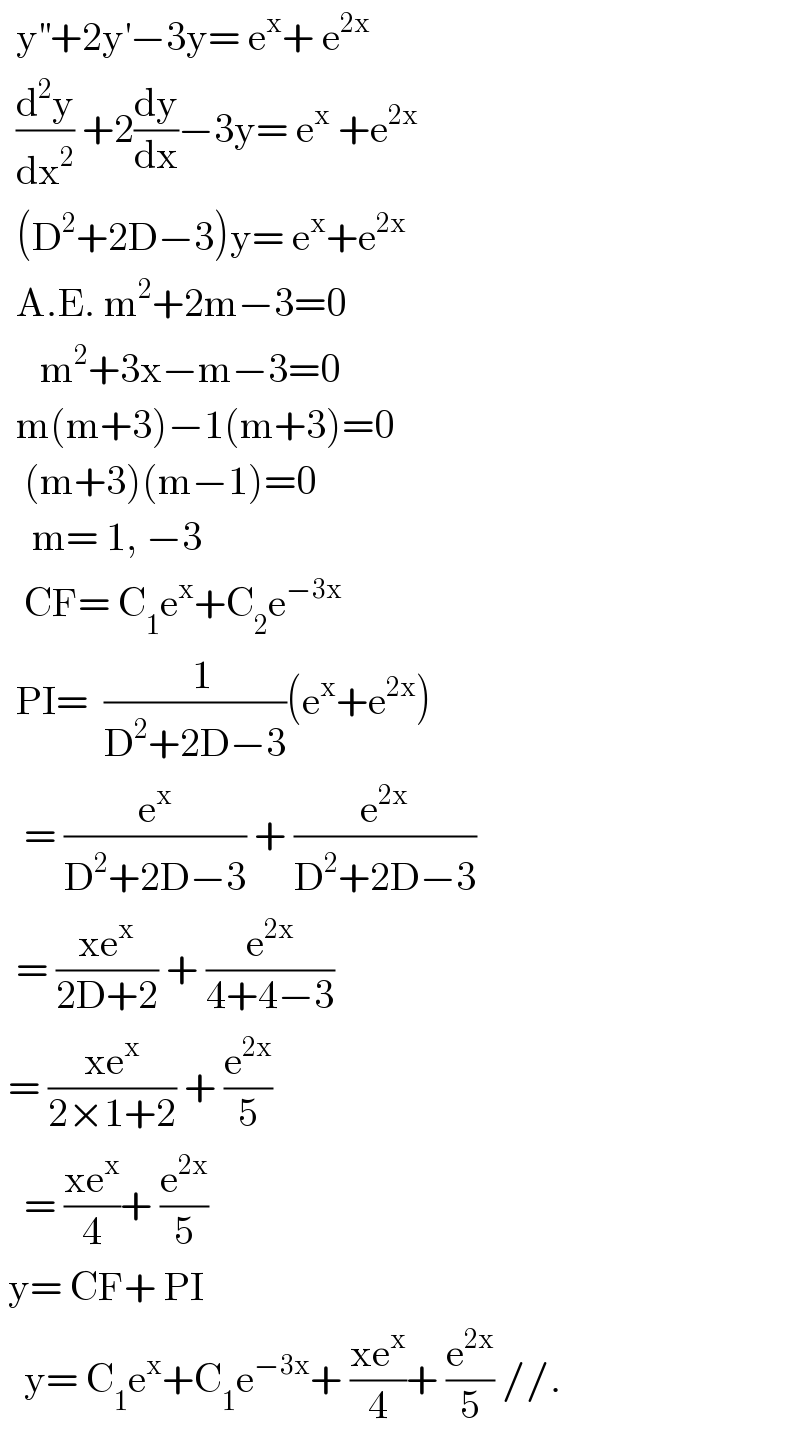
y^(′′) +2y^′ −3y= e^x + e^(2x) (d^2 y/dx^2 ) +2(dy/dx)−3y= e^x +e^(2x) (D^2 +2D−3)y= e^x +e^(2x) A.E. m^2 +2m−3=0 m^2 +3x−m−3=0 m(m+3)−1(m+3)=0 (m+3)(m−1)=0 m= 1, −3 CF= C_1 e^x +C_2 e^(−3x) PI= (( 1)/(D^2 +2D−3))(e^x +e^(2x) ) = (e^x /(D^2 +2D−3)) + (e^(2x) /(D^2 +2D−3)) = ((xe^x )/(2D+2)) + (e^(2x) /(4+4−3)) = ((xe^x )/(2×1+2)) + (e^(2x) /5) = ((xe^x )/4)+ (e^(2x) /5) y= CF+ PI y= C_1 e^x +C_1 e^(−3x) + ((xe^x )/4)+ (e^(2x) /5) //.
$$\:\:\mathrm{y}^{''} +\mathrm{2y}^{'} −\mathrm{3y}=\:\mathrm{e}^{\mathrm{x}} +\:\mathrm{e}^{\mathrm{2x}} \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\mathrm{2}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{3y}=\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{\mathrm{2x}} \\ $$$$\:\:\left(\mathrm{D}^{\mathrm{2}} +\mathrm{2D}−\mathrm{3}\right)\mathrm{y}=\:\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{\mathrm{2x}} \\ $$$$\:\:\mathrm{A}.\mathrm{E}.\:\mathrm{m}^{\mathrm{2}} +\mathrm{2m}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{m}^{\mathrm{2}} +\mathrm{3x}−\mathrm{m}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\mathrm{m}\left(\mathrm{m}+\mathrm{3}\right)−\mathrm{1}\left(\mathrm{m}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\:\left(\mathrm{m}+\mathrm{3}\right)\left(\mathrm{m}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{m}=\:\mathrm{1},\:−\mathrm{3} \\ $$$$\:\:\:\mathrm{CF}=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{3x}} \\ $$$$\:\:\mathrm{PI}=\:\:\frac{\:\:\mathrm{1}}{\mathrm{D}^{\mathrm{2}} +\mathrm{2D}−\mathrm{3}}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{\mathrm{2x}} \right) \\ $$$$\:\:\:=\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{D}^{\mathrm{2}} +\mathrm{2D}−\mathrm{3}}\:+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{D}^{\mathrm{2}} +\mathrm{2D}−\mathrm{3}} \\ $$$$\:\:=\:\frac{\mathrm{xe}^{\mathrm{x}} }{\mathrm{2D}+\mathrm{2}}\:+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{4}+\mathrm{4}−\mathrm{3}} \\ $$$$\:=\:\frac{\mathrm{xe}^{\mathrm{x}} }{\mathrm{2}×\mathrm{1}+\mathrm{2}}\:+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}} \\ $$$$\:\:\:=\:\frac{\mathrm{xe}^{\mathrm{x}} }{\mathrm{4}}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}} \\ $$$$\:\mathrm{y}=\:\mathrm{CF}+\:\mathrm{PI} \\ $$$$\:\:\:\mathrm{y}=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{3x}} +\:\frac{\mathrm{xe}^{\mathrm{x}} }{\mathrm{4}}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\://. \\ $$
Answered by Rio Michael last updated on 08/May/20
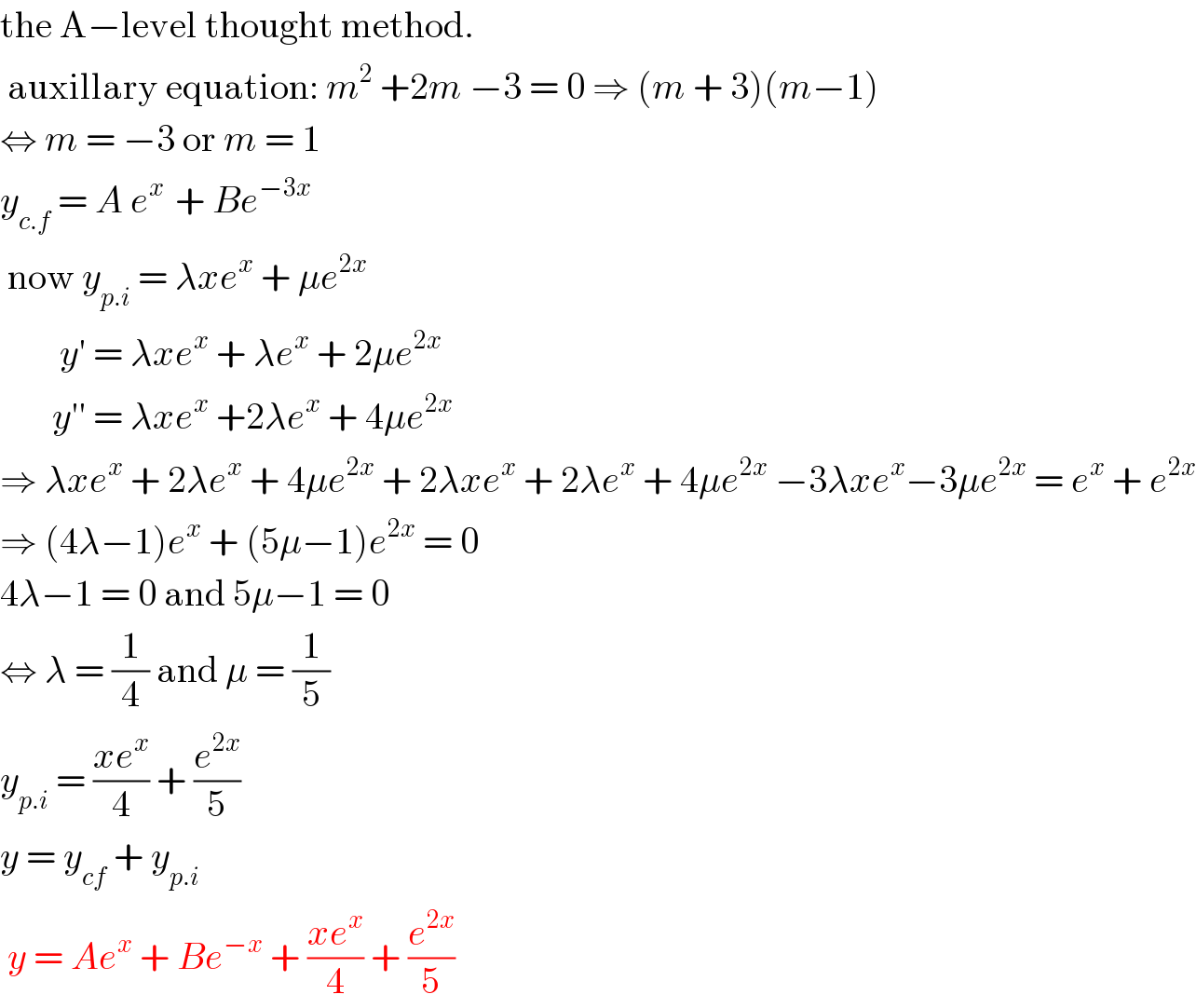
the A−level thought method. auxillary equation: m^2 +2m −3 = 0 ⇒ (m + 3)(m−1) ⇔ m = −3 or m = 1 y_(c.f) = A e^(x ) + Be^(−3x) now y_(p.i) = λxe^x + μe^(2x) y′ = λxe^x + λe^x + 2μe^(2x) y′′ = λxe^x +2λe^x + 4μe^(2x) ⇒ λxe^x + 2λe^x + 4μe^(2x) + 2λxe^x + 2λe^x + 4μe^(2x) −3λxe^x −3μe^(2x) = e^x + e^(2x) ⇒ (4λ−1)e^x + (5μ−1)e^(2x) = 0 4λ−1 = 0 and 5μ−1 = 0 ⇔ λ = (1/4) and μ = (1/5) y_(p.i) = ((xe^x )/4) + (e^(2x) /5) y = y_(cf) + y_(p.i) y = Ae^x + Be^(−x) + ((xe^x )/4) + (e^(2x) /5)
$$\mathrm{the}\:\mathrm{A}−\mathrm{level}\:\mathrm{thought}\:\mathrm{method}. \\ $$$$\:\mathrm{auxillary}\:\mathrm{equation}:\:{m}^{\mathrm{2}} \:+\mathrm{2}{m}\:−\mathrm{3}\:=\:\mathrm{0}\:\Rightarrow\:\left({m}\:+\:\mathrm{3}\right)\left({m}−\mathrm{1}\right)\: \\ $$$$\Leftrightarrow\:{m}\:=\:−\mathrm{3}\:\mathrm{or}\:{m}\:=\:\mathrm{1} \\ $$$${y}_{{c}.{f}} \:=\:{A}\:{e}^{{x}\:} \:+\:{Be}^{−\mathrm{3}{x}} \\ $$$$\:\mathrm{now}\:{y}_{{p}.{i}} \:=\:\lambda{xe}^{{x}} \:+\:\mu{e}^{\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:\:{y}'\:=\:\lambda{xe}^{{x}} \:+\:\lambda{e}^{{x}} \:+\:\mathrm{2}\mu{e}^{\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:{y}''\:=\:\lambda{xe}^{{x}} \:+\mathrm{2}\lambda{e}^{{x}} \:+\:\mathrm{4}\mu{e}^{\mathrm{2}{x}} \\ $$$$\Rightarrow\:\lambda{xe}^{{x}} \:+\:\mathrm{2}\lambda{e}^{{x}} \:+\:\mathrm{4}\mu{e}^{\mathrm{2}{x}} \:+\:\mathrm{2}\lambda{xe}^{{x}} \:+\:\mathrm{2}\lambda{e}^{{x}} \:+\:\mathrm{4}\mu{e}^{\mathrm{2}{x}} \:−\mathrm{3}\lambda{xe}^{{x}} −\mathrm{3}\mu{e}^{\mathrm{2}{x}} \:=\:{e}^{{x}} \:+\:{e}^{\mathrm{2}{x}} \\ $$$$\Rightarrow\:\left(\mathrm{4}\lambda−\mathrm{1}\right){e}^{{x}} \:+\:\left(\mathrm{5}\mu−\mathrm{1}\right){e}^{\mathrm{2}{x}} \:=\:\mathrm{0} \\ $$$$\mathrm{4}\lambda−\mathrm{1}\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{5}\mu−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\lambda\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{and}\:\mu\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${y}_{{p}.{i}} \:=\:\frac{{xe}^{{x}} }{\mathrm{4}}\:+\:\frac{{e}^{\mathrm{2}{x}} }{\mathrm{5}} \\ $$$${y}\:=\:{y}_{{cf}} \:+\:{y}_{{p}.{i}} \\ $$$$\:{y}\:=\:{Ae}^{{x}} \:+\:{Be}^{−{x}} \:+\:\frac{{xe}^{{x}} }{\mathrm{4}}\:+\:\frac{{e}^{\mathrm{2}{x}} }{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *