Question Number 91287 by jagoll last updated on 29/Apr/20
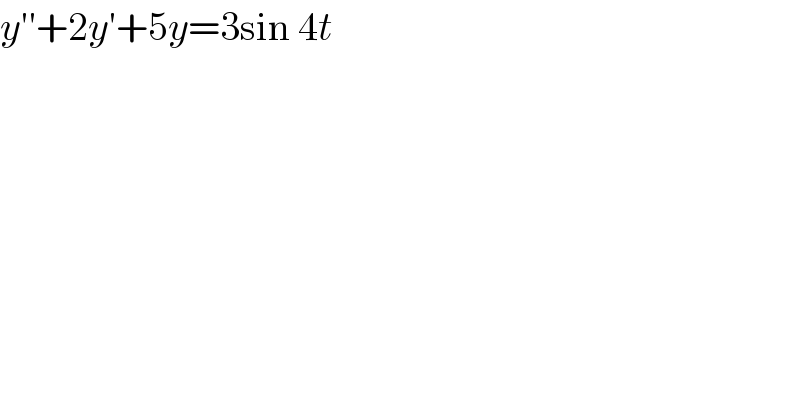
$${y}''+\mathrm{2}{y}'+\mathrm{5}{y}=\mathrm{3sin}\:\mathrm{4}{t} \\ $$
Answered by niroj last updated on 29/Apr/20

$$\:\:\:\mathrm{y}^{''} +\mathrm{2y}'+\mathrm{5y}=\:\mathrm{3sin}\:\mathrm{4t} \\ $$$$\:\:\left(\mathrm{D}^{\mathrm{2}} +\mathrm{2D}+\mathrm{5}\right)\mathrm{y}=\:\mathrm{3sin}\:\mathrm{4t}\:\: \\ $$$$\:\:\mathrm{A}.\mathrm{E}.,\:\mathrm{m}^{\mathrm{2}} +\mathrm{2m}+\mathrm{5}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{m}=\:−\mathrm{1}\overset{−} {+}\mathrm{2i} \\ $$$$\:\:\mathrm{CF}\:=\:\:\mathrm{e}^{−\mathrm{t}} \left(\mathrm{Acos2t}+\mathrm{Bsin2t}\right) \\ $$$$\:\:\mathrm{PI}=\:\:\frac{\mathrm{3sin4t}}{\mathrm{D}^{\mathrm{2}} +\mathrm{2D}+\mathrm{5}}=\:\frac{\mathrm{3sin4t}}{−\mathrm{16}+\mathrm{2D}+\mathrm{5}} \\ $$$$\:\:\:\:=\:\frac{\mathrm{3sin4t}}{\mathrm{2D}−\mathrm{11}}=\:\frac{\left(\mathrm{2D}+\mathrm{11}\right)\mathrm{3sin4t}}{\mathrm{4D}^{\mathrm{2}} −\mathrm{121}} \\ $$$$\:\:\:=\:\:\frac{\left(\mathrm{2D}+\mathrm{11}\right)\mathrm{3sin4t}}{−\mathrm{64}−\mathrm{121}}=\:−\frac{\mathrm{1}}{\mathrm{185}}\left(\mathrm{24cos4t}+\mathrm{33sin4t}\right) \\ $$$$\:\mathrm{y}=\mathrm{CF}+\mathrm{PI} \\ $$$$\:\mathrm{y}=\:\mathrm{e}^{−\mathrm{t}} \left(\mathrm{Acos2t}+\mathrm{Bsin2t}\right)−\:\frac{\mathrm{1}}{\mathrm{185}}\left(\:\mathrm{24cos4t}+\:\mathrm{33}\:\mathrm{sin4t}\right) \\ $$$$ \\ $$
Commented by jagoll last updated on 29/Apr/20
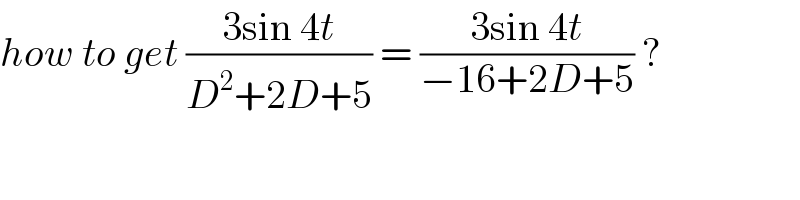
$${how}\:{to}\:{get}\:\frac{\mathrm{3sin}\:\mathrm{4}{t}}{{D}^{\mathrm{2}} +\mathrm{2}{D}+\mathrm{5}}\:=\:\frac{\mathrm{3sin}\:\mathrm{4}{t}}{−\mathrm{16}+\mathrm{2}{D}+\mathrm{5}}\:? \\ $$
Commented by niroj last updated on 29/Apr/20
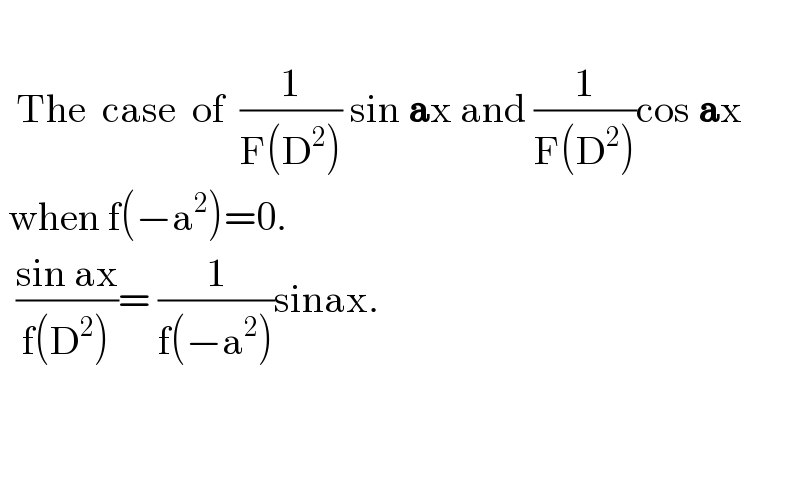
$$ \\ $$$$\:\:\mathrm{The}\:\:\mathrm{case}\:\:\mathrm{of}\:\:\frac{\mathrm{1}}{\mathrm{F}\left(\mathrm{D}^{\mathrm{2}} \right)}\:\mathrm{sin}\:\boldsymbol{\mathrm{a}}\mathrm{x}\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{F}\left(\mathrm{D}^{\mathrm{2}} \right)}\mathrm{cos}\:\boldsymbol{\mathrm{a}}\mathrm{x} \\ $$$$\:\mathrm{when}\:\mathrm{f}\left(−\mathrm{a}^{\mathrm{2}} \right)=\mathrm{0}. \\ $$$$\:\:\frac{\mathrm{sin}\:\mathrm{ax}}{\mathrm{f}\left(\mathrm{D}^{\mathrm{2}} \right)}=\:\frac{\mathrm{1}}{\mathrm{f}\left(−\mathrm{a}^{\mathrm{2}} \right)}\mathrm{sinax}. \\ $$$$ \\ $$$$\: \\ $$
