Question Number 128420 by bramlexs22 last updated on 07/Jan/21
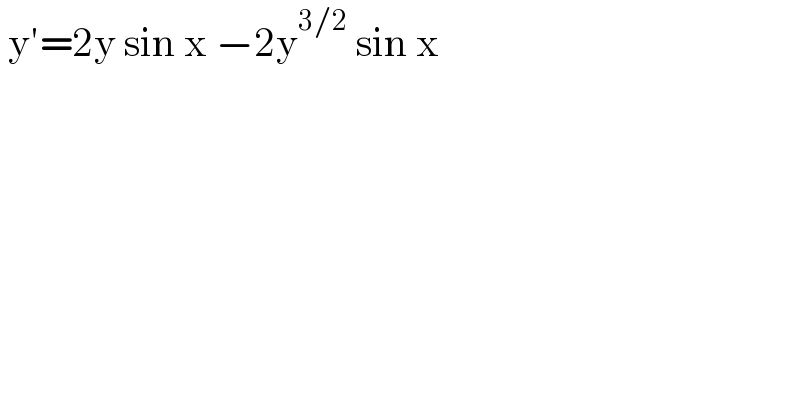
$$\:\mathrm{y}'=\mathrm{2y}\:\mathrm{sin}\:\mathrm{x}\:−\mathrm{2y}^{\mathrm{3}/\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}\: \\ $$
Answered by liberty last updated on 07/Jan/21
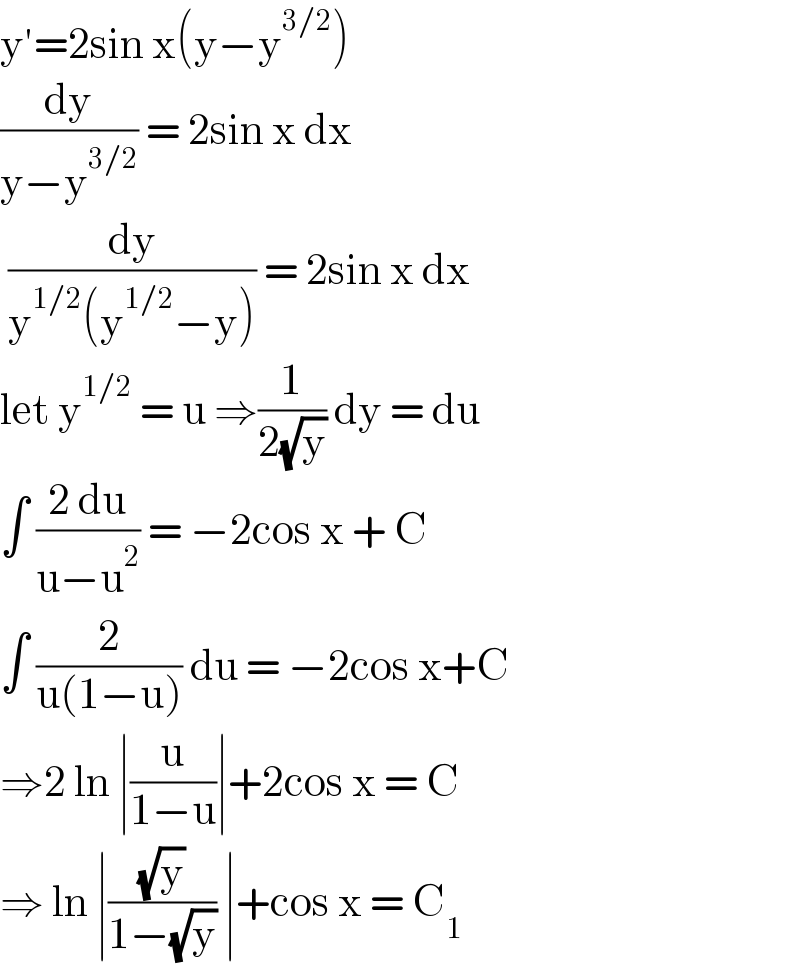
$$\mathrm{y}'=\mathrm{2sin}\:\mathrm{x}\left(\mathrm{y}−\mathrm{y}^{\mathrm{3}/\mathrm{2}} \right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{y}−\mathrm{y}^{\mathrm{3}/\mathrm{2}} }\:=\:\mathrm{2sin}\:\mathrm{x}\:\mathrm{dx}\: \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{1}/\mathrm{2}} \left(\mathrm{y}^{\mathrm{1}/\mathrm{2}} −\mathrm{y}\right)}\:=\:\mathrm{2sin}\:\mathrm{x}\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{y}^{\mathrm{1}/\mathrm{2}} \:=\:\mathrm{u}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{y}}}\:\mathrm{dy}\:=\:\mathrm{du}\: \\ $$$$\int\:\frac{\mathrm{2}\:\mathrm{du}}{\mathrm{u}−\mathrm{u}^{\mathrm{2}} }\:=\:−\mathrm{2cos}\:\mathrm{x}\:+\:\mathrm{C} \\ $$$$\int\:\frac{\mathrm{2}}{\mathrm{u}\left(\mathrm{1}−\mathrm{u}\right)}\:\mathrm{du}\:=\:−\mathrm{2cos}\:\mathrm{x}+\mathrm{C} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{ln}\:\mid\frac{\mathrm{u}}{\mathrm{1}−\mathrm{u}}\mid+\mathrm{2cos}\:\mathrm{x}\:=\:\mathrm{C}\: \\ $$$$\Rightarrow\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{y}}}{\mathrm{1}−\sqrt{\mathrm{y}}}\:\mid+\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{C}_{\mathrm{1}} \\ $$
