Menu Close

y-2y-y-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 91911 by jagoll last updated on 03/May/20
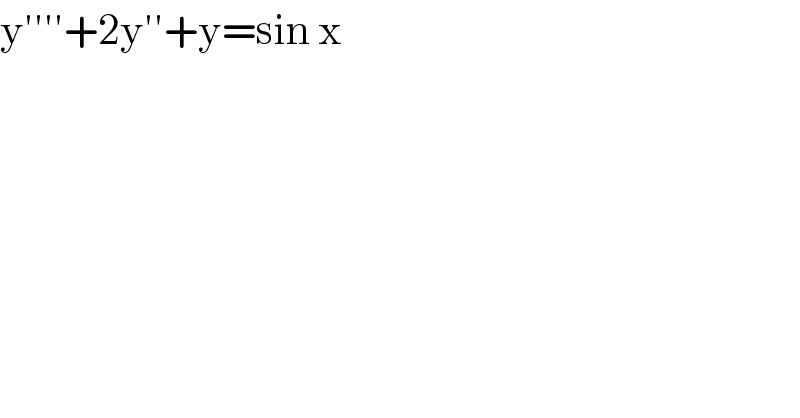
y′′′′+2y′′+y=sin x
$$\mathrm{y}''''+\mathrm{2y}''+\mathrm{y}=\mathrm{sin}\:\mathrm{x}\: \\ $$
Answered by niroj last updated on 03/May/20
y^(′′′′) +2y^(′′) +y= sin x (d^4 y/dx^4 )+2(d^2 y/dx^2 )+y= sin x (D^4 +2D^2 +1)y= sin x A.E., m^4 +2m^2 +1=0 (m^2 +1)^2 =0 m=0+^− i,0+^− i CF= (C_1 x+C_2 )cos x+(C_3 x+C_4 )sinx PI= ((sin x)/(D^4 +2D^2 +1))= ((sin x)/((D^2 +1)^2 )) = ((x sin x)/(4D^3 +4D))= ((x sin x)/(2(D^2 +1)2D)) = ((x^2 sinx)/(12D^2 +4))= (( x^2 sinx)/(4(3D^2 +1))) = (((3D^2 −1)x^2 sin x)/(4(9D^2 −1))) = (((3D^2 −1)x^2 sin x)/(4(−9−1)))= − (1/(40))(3D^2 −1)x^2 sinx −(1/(40))(6 sin x+12x cos x −3x^2 sin x−x^2 sin x) −(1/(40))(6 sin x +12 x cos x−4x^2 sinx) y = (C_1 x+C_2 )cos x+(C_2 x+C_4 )sin x −(1/(40))(6 sin x+12x cos x−4x^2 sin x)
$$\:\:\mathrm{y}^{''''} +\mathrm{2y}^{''} +\mathrm{y}=\:\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\:\frac{\mathrm{d}^{\mathrm{4}} \mathrm{y}}{\mathrm{dx}^{\mathrm{4}} }+\mathrm{2}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{y}=\:\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\left(\mathrm{D}^{\mathrm{4}} +\mathrm{2D}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{y}=\:\mathrm{sin}\:\mathrm{x} \\ $$$$\:\mathrm{A}.\mathrm{E}.,\:\:\mathrm{m}^{\mathrm{4}} +\mathrm{2m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left(\mathrm{m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\mathrm{m}=\mathrm{0}\overset{−} {+}\mathrm{i},\mathrm{0}\overset{−} {+}\mathrm{i} \\ $$$$\:\:\:\mathrm{CF}=\:\left(\mathrm{C}_{\mathrm{1}} \mathrm{x}+\mathrm{C}_{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{x}+\left(\mathrm{C}_{\mathrm{3}} \mathrm{x}+\mathrm{C}_{\mathrm{4}} \right)\mathrm{sinx} \\ $$$$\:\:\mathrm{PI}=\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{D}^{\mathrm{4}} +\mathrm{2D}^{\mathrm{2}} +\mathrm{1}}=\:\frac{\mathrm{sin}\:\mathrm{x}}{\left(\mathrm{D}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{4D}^{\mathrm{3}} +\mathrm{4D}}=\:\frac{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{2}\left(\mathrm{D}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{2D}} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{sinx}}{\mathrm{12D}^{\mathrm{2}} +\mathrm{4}}=\:\frac{\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sinx}}{\mathrm{4}\left(\mathrm{3D}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\:\:=\:\frac{\left(\mathrm{3D}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}}{\mathrm{4}\left(\mathrm{9D}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\:\:=\:\frac{\left(\mathrm{3D}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}}{\mathrm{4}\left(−\mathrm{9}−\mathrm{1}\right)}=\:−\:\frac{\mathrm{1}}{\mathrm{40}}\left(\mathrm{3D}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} \mathrm{sinx} \\ $$$$\:\:−\frac{\mathrm{1}}{\mathrm{40}}\left(\mathrm{6}\:\mathrm{sin}\:\mathrm{x}+\mathrm{12x}\:\mathrm{cos}\:\mathrm{x}\:−\mathrm{3x}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\:−\frac{\mathrm{1}}{\mathrm{40}}\left(\mathrm{6}\:\mathrm{sin}\:\mathrm{x}\:\:+\mathrm{12}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}−\mathrm{4x}^{\mathrm{2}} \:\mathrm{sinx}\right) \\ $$$$\:\:\mathrm{y}\:=\:\left(\mathrm{C}_{\mathrm{1}} \mathrm{x}+\mathrm{C}_{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{x}+\left(\mathrm{C}_{\mathrm{2}} \mathrm{x}+\mathrm{C}_{\mathrm{4}} \right)\mathrm{sin}\:\mathrm{x}\:−\frac{\mathrm{1}}{\mathrm{40}}\left(\mathrm{6}\:\mathrm{sin}\:\mathrm{x}+\mathrm{12x}\:\mathrm{cos}\:\mathrm{x}−\mathrm{4x}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *