Question Number 51709 by sinx last updated on 29/Dec/18
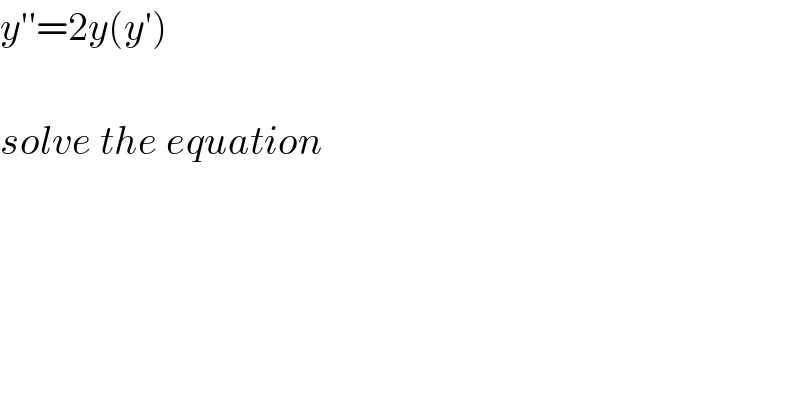
$${y}''=\mathrm{2}{y}\left({y}'\right) \\ $$$$ \\ $$$${solve}\:{the}\:{equation} \\ $$
Answered by mr W last updated on 29/Dec/18
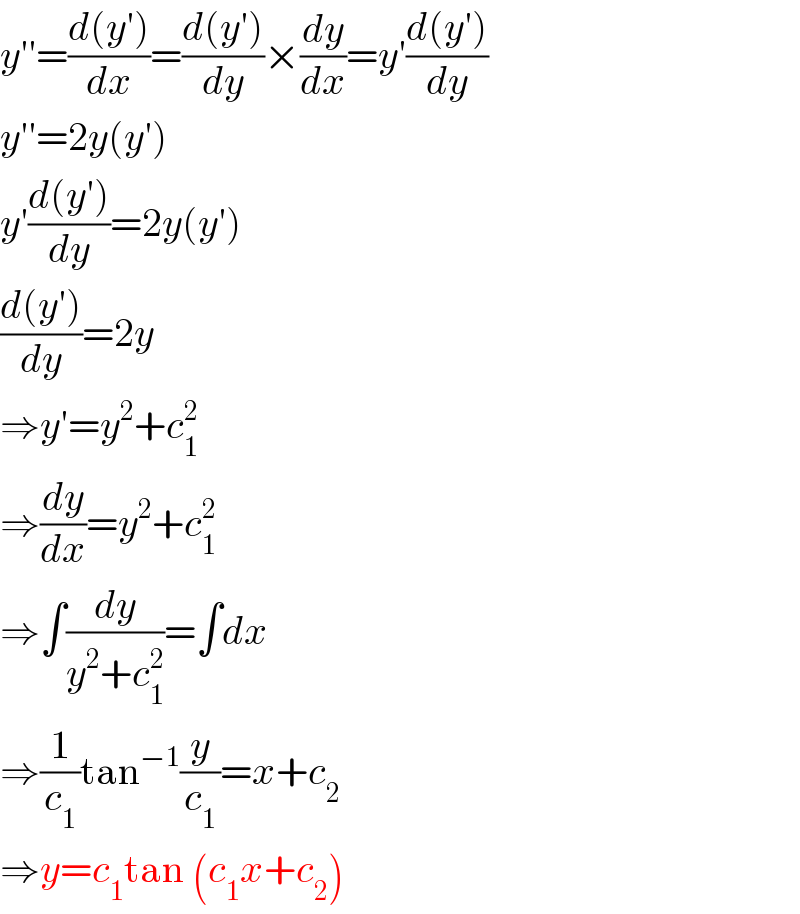
$${y}''=\frac{{d}\left({y}'\right)}{{dx}}=\frac{{d}\left({y}'\right)}{{dy}}×\frac{{dy}}{{dx}}={y}'\frac{{d}\left({y}'\right)}{{dy}} \\ $$$${y}''=\mathrm{2}{y}\left({y}'\right) \\ $$$${y}'\frac{{d}\left({y}'\right)}{{dy}}=\mathrm{2}{y}\left({y}'\right) \\ $$$$\frac{{d}\left({y}'\right)}{{dy}}=\mathrm{2}{y} \\ $$$$\Rightarrow{y}'={y}^{\mathrm{2}} +{c}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={y}^{\mathrm{2}} +{c}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow\int\frac{{dy}}{{y}^{\mathrm{2}} +{c}_{\mathrm{1}} ^{\mathrm{2}} }=\int{dx} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{c}_{\mathrm{1}} }\mathrm{tan}^{−\mathrm{1}} \frac{{y}}{{c}_{\mathrm{1}} }={x}+{c}_{\mathrm{2}} \\ $$$$\Rightarrow{y}={c}_{\mathrm{1}} \mathrm{tan}\:\left({c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} \right) \\ $$
Answered by Abdulhafeez Abu qatada last updated on 30/Dec/18
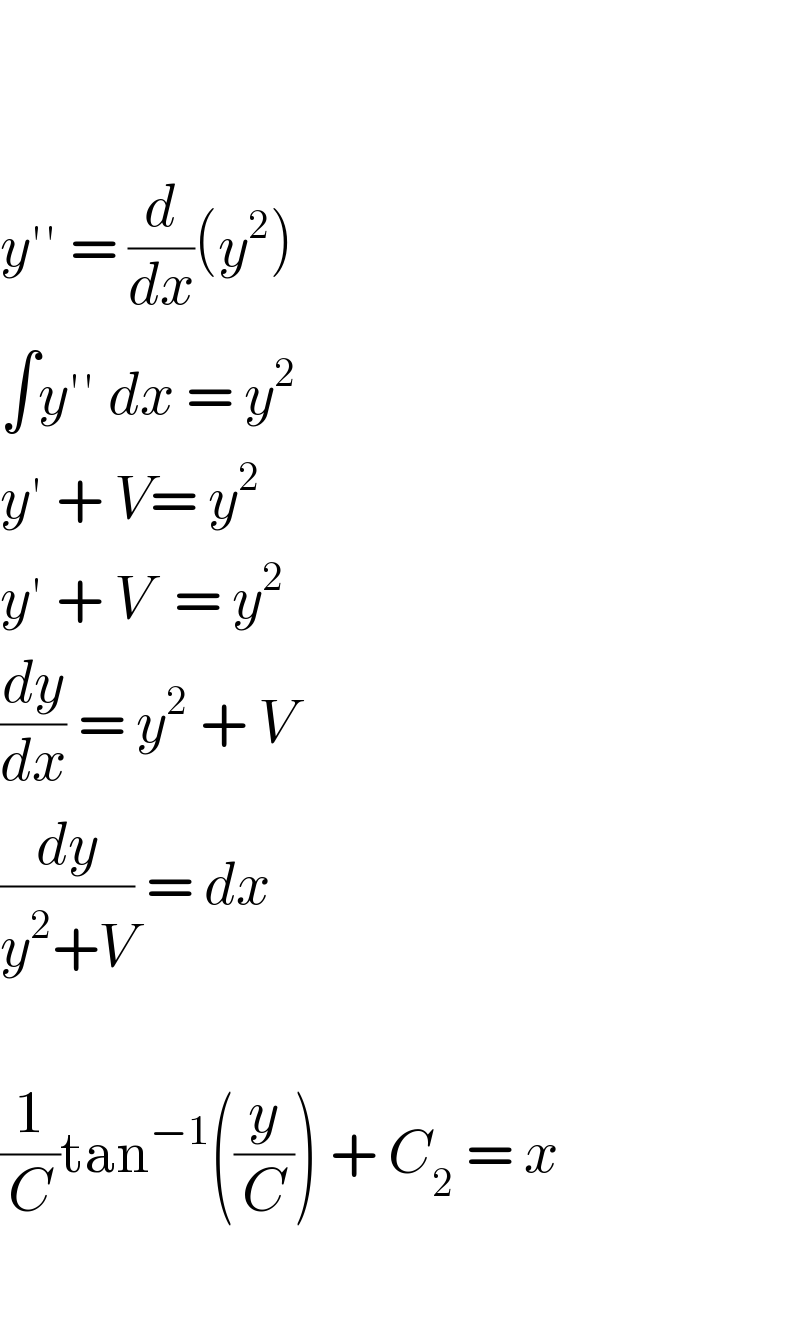
$$ \\ $$$$ \\ $$$${y}''\:=\:\frac{{d}}{{dx}}\left({y}^{\mathrm{2}} \right) \\ $$$$\int{y}''\:{dx}\:=\:{y}^{\mathrm{2}} \\ $$$${y}'\:+\:{V}=\:{y}^{\mathrm{2}} \\ $$$${y}'\:+\:{V}\:\:=\:{y}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}\:=\:{y}^{\mathrm{2}} \:+\:{V} \\ $$$$\frac{{dy}}{{y}^{\mathrm{2}} +{V}}\:=\:{dx} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{C}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{C}}\right)\:+\:{C}_{\mathrm{2}} \:=\:{x}\: \\ $$$$ \\ $$
