y-3y-10y-14e-5x-

Question Number 102716 by Ar Brandon last updated on 10/Jul/20

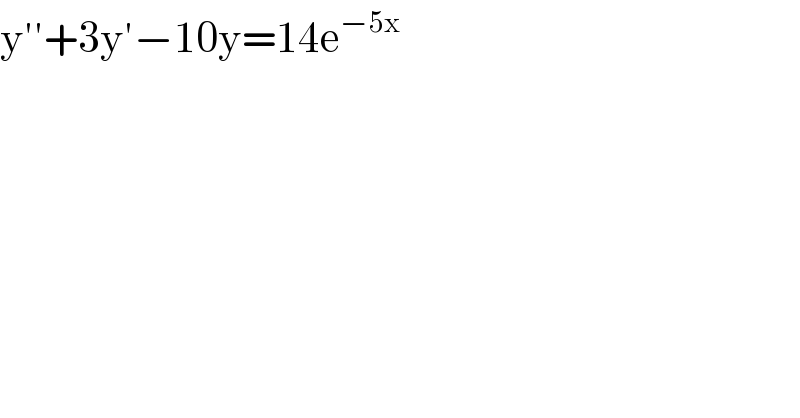
$$\mathrm{y}''+\mathrm{3y}'−\mathrm{10y}=\mathrm{14e}^{−\mathrm{5x}} \\ $$

Answered by bramlex last updated on 10/Jul/20

Homogenous r^2 +3r−10=0 ⇒(r+5)(r−2)=0 y_h = Ae^(2x) +Be^(−5x) PI. y_p = Cxe^(−5x) ; y′ = Ce^(−5x) −5Cxe^(−5x) y′′=−5Ce^(−5x) −5C(e^(−5x) −5xe^(−5x) ) y′′=−10Ce^(−5x) +25Cxe^(−5x) comparing coefficient −10Ce^(−5x) +25Cxe^(−5x) +3Ce^(−5x) −15Cxe^(−5x) −10Cxe^(−5x) =14e^(−5x) ⇒−7Ce^(−5x) =14e^(−5x) ⇒C=−2 y_p =−2xe^(−5x) ∴generall solution y= Ae^(2x) +Be^(−5x) −2xe^(−5x) ▼^(°⌢•⌢)

$$\mathrm{Homogenous}\: \\ $$$$\mathrm{r}^{\mathrm{2}} +\mathrm{3r}−\mathrm{10}=\mathrm{0}\:\Rightarrow\left(\mathrm{r}+\mathrm{5}\right)\left(\mathrm{r}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{\mathrm{2x}} +\mathrm{Be}^{−\mathrm{5x}} \\ $$$$\mathrm{PI}.\:\mathrm{y}_{\mathrm{p}} \:=\:\mathrm{Cxe}^{−\mathrm{5x}} \:;\:\mathrm{y}'\:=\:\mathrm{Ce}^{−\mathrm{5x}} −\mathrm{5Cxe}^{−\mathrm{5x}} \\ $$$$\mathrm{y}''=−\mathrm{5Ce}^{−\mathrm{5x}} −\mathrm{5C}\left(\mathrm{e}^{−\mathrm{5x}} −\mathrm{5xe}^{−\mathrm{5x}} \right) \\ $$$$\mathrm{y}''=−\mathrm{10Ce}^{−\mathrm{5x}} +\mathrm{25Cxe}^{−\mathrm{5x}} \\ $$$$\mathrm{comparing}\:\mathrm{coefficient} \\ $$$$−\mathrm{10Ce}^{−\mathrm{5x}} +\mathrm{25Cxe}^{−\mathrm{5x}} +\mathrm{3Ce}^{−\mathrm{5x}} −\mathrm{15Cxe}^{−\mathrm{5x}} −\mathrm{10Cxe}^{−\mathrm{5x}} =\mathrm{14e}^{−\mathrm{5x}} \\ $$$$\Rightarrow−\mathrm{7Ce}^{−\mathrm{5x}} =\mathrm{14e}^{−\mathrm{5x}} \:\Rightarrow\mathrm{C}=−\mathrm{2} \\ $$$$\mathrm{y}_{\mathrm{p}} =−\mathrm{2xe}^{−\mathrm{5x}} \\ $$$$\therefore\mathrm{generall}\:\mathrm{solution}\: \\ $$$$\mathrm{y}=\:\mathrm{Ae}^{\mathrm{2x}} +\mathrm{Be}^{−\mathrm{5x}} −\mathrm{2xe}^{−\mathrm{5x}} \: \\ $$$$\overset{°\frown\bullet\frown} {\blacktrinagledown} \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

�� Thanks

Commented by bramlex last updated on 10/Jul/20

$$\mathrm{because}\:\mathrm{e}^{−\mathrm{5x}} \:\mathrm{is}\:\mathrm{homogenous} \\ $$$$\mathrm{solution} \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

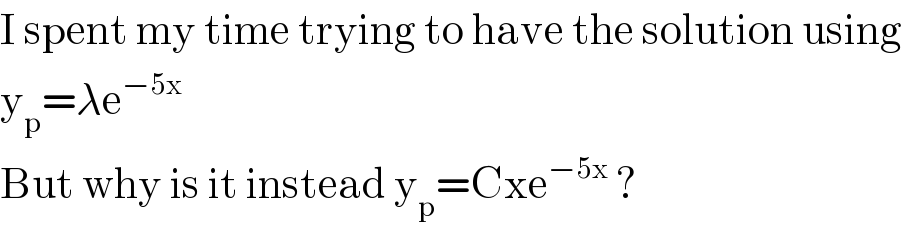
I spent my time trying to have the solution using y_p =λe^(−5x) But why is it instead y_p =Cxe^(−5x) ?

$$\mathrm{I}\:\mathrm{spent}\:\mathrm{my}\:\mathrm{time}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{have}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{using} \\ $$$$\mathrm{y}_{\mathrm{p}} =\lambda\mathrm{e}^{−\mathrm{5x}} \\ $$$$\mathrm{But}\:\mathrm{why}\:\mathrm{is}\:\mathrm{it}\:\mathrm{instead}\:\mathrm{y}_{\mathrm{p}} =\mathrm{Cxe}^{−\mathrm{5x}} \:? \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

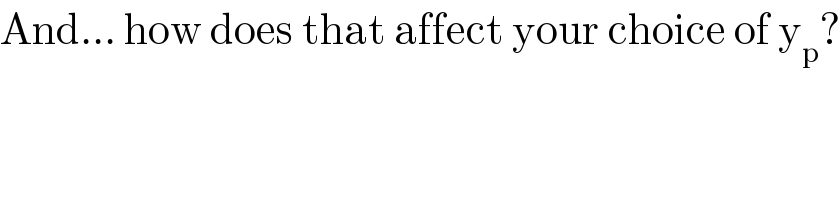
And... how does that affect your choice of y_p ?

$$\mathrm{And}…\:\mathrm{how}\:\mathrm{does}\:\mathrm{that}\:\mathrm{affect}\:\mathrm{your}\:\mathrm{choice}\:\mathrm{of}\:\mathrm{y}_{\mathrm{p}} ? \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

OK I think I′ve understood. I completely forgot about that. The form λe^(−5x) is already present in the Complementary function and it′s pointless having it again in y_p . So we therefore move to the higher degree of x.

$$\mathrm{OK}\:\mathrm{I}\:\mathrm{think}\:\mathrm{I}'\mathrm{ve}\:\mathrm{understood}.\:\mathrm{I}\:\mathrm{completely}\:\mathrm{forgot}\: \\ $$$$\mathrm{about}\:\mathrm{that}.\:\mathrm{The}\:\mathrm{form}\:\lambda\mathrm{e}^{−\mathrm{5x}} \:\mathrm{is}\:\mathrm{already}\:\mathrm{present}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{Complementary}\:\mathrm{function}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{pointless}\:\mathrm{having} \\ $$$$\mathrm{it}\:\mathrm{again}\:\mathrm{in}\:\mathrm{y}_{\mathrm{p}} .\:\mathrm{So}\:\mathrm{we}\:\mathrm{therefore}\:\mathrm{move}\:\mathrm{to}\:\mathrm{the}\:\mathrm{higher} \\ $$$$\mathrm{degree}\:\mathrm{of}\:\mathrm{x}. \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

�� Thanks

Commented by Ar Brandon last updated on 10/Jul/20

https://www.pdfdrive.com/search?q=jee+mathematics&pagecount=&pubyear=&searchin=

Commented by Dwaipayan Shikari last updated on 10/Jul/20

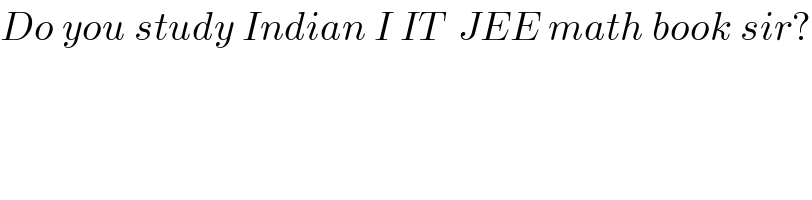
$${Do}\:{you}\:{study}\:{Indian}\:{I}\:{IT}\:\:{JEE}\:{math}\:{book}\:{sir}? \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

Yes bro,�� They're among my ebooks.��

Commented by Dwaipayan Shikari last updated on 10/Jul/20

Oh I am a Indian student also��.Which book do you study?��

Commented by Ar Brandon last updated on 10/Jul/20

��From your name I could deduce that.

Commented by Ar Brandon last updated on 10/Jul/20

But actually I just use these JEE Ebooks to help maximise my skills. I noticed it contains questions which push you to the peak of reasoning in every chapter.And I'm also a student.��

Commented by Dwaipayan Shikari last updated on 10/Jul/20

�� I am also.......( understand what I want to mean)

Commented by Ar Brandon last updated on 10/Jul/20

��

Commented by IRAN_majid last updated on 10/Jul/20

$${ok} \\ $$

Answered by mathmax by abdo last updated on 10/Jul/20

wronskien method he→y^(′′) +3y^′ −10y =0 ⇒r^2 +3r−10 =0 Δ =9−4(−10) =49 ⇒r_1 =((−3+7)/2) =2 and r_2 =((−3−7)/2) =−5 ⇒ ⇒y_h =a e^(2x) +b e^(−5x) =au_1 +bu_2 w(u_1 ,u_2 ) = determinant (((e^(2x) e^(−5x) )),((2e^(2x) −5 e^(−5x) ))) =−5 e^(−3x) −2e^(−3x) =−7 e^(−3x) W_1 = determinant (((0 e^(−5x) )),((14 e^(−5x) −5e^(−5x) ))) =−14 e^(−10x) W_2 = determinant (((e^(2x) 0)),((2e^(2x) 14 e^(−5x) ))) =14e^(−3x) v_1 =∫ (w_1 /W)dx =∫ ((−14 e^(−10x) )/(−7 e^(−3x) )) dx = 2 ∫ e^(−7x) dx =−(2/7)e^(−7x) v_2 =∫ (W_2 /W) dx =∫ ((14e^(−3x) )/(−7e^(−3x) ))dx =−2 x ⇒ y_p =u_1 v_1 +u_2 v_2 =e^(2x) ×(−(2/7))e^(−7x) + e^(−5x) ×(−2x) =−(2/7) e^(−7x) −2x e^(−5x) ⇒ the general solution is y =y_h +y_p y = ae^(2x) +b e^(−5x) −(2/7) e^(−7x) −2x e^(−5x)

$$\mathrm{wronskien}\:\mathrm{method} \\ $$$$\mathrm{he}\rightarrow\mathrm{y}^{''} +\mathrm{3y}^{'} −\mathrm{10y}\:=\mathrm{0}\:\Rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{3r}−\mathrm{10}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{9}−\mathrm{4}\left(−\mathrm{10}\right)\:=\mathrm{49}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{−\mathrm{3}+\mathrm{7}}{\mathrm{2}}\:=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{−\mathrm{3}−\mathrm{7}}{\mathrm{2}}\:=−\mathrm{5}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{2x}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{5x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{w}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{5x}} }\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:−\mathrm{5}\:\mathrm{e}^{−\mathrm{5x}} }\end{vmatrix}\:=−\mathrm{5}\:\mathrm{e}^{−\mathrm{3x}} −\mathrm{2e}^{−\mathrm{3x}} \:=−\mathrm{7}\:\mathrm{e}^{−\mathrm{3x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{5x}} }\\{\mathrm{14}\:\mathrm{e}^{−\mathrm{5x}} \:\:\:\:\:\:\:\:\:\:\:−\mathrm{5e}^{−\mathrm{5x}} }\end{vmatrix}\:=−\mathrm{14}\:\mathrm{e}^{−\mathrm{10x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\:\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\:\:\mathrm{14}\:\mathrm{e}^{−\mathrm{5x}} }\end{vmatrix}\:=\mathrm{14e}^{−\mathrm{3x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{14}\:\mathrm{e}^{−\mathrm{10x}} }{−\mathrm{7}\:\mathrm{e}^{−\mathrm{3x}} }\:\mathrm{dx}\:=\:\mathrm{2}\:\int\:\mathrm{e}^{−\mathrm{7x}} \:\mathrm{dx}\:=−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{e}^{−\mathrm{7x}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\:\mathrm{dx}\:=\int\:\frac{\mathrm{14e}^{−\mathrm{3x}} }{−\mathrm{7e}^{−\mathrm{3x}} }\mathrm{dx}\:=−\mathrm{2}\:\mathrm{x}\:\Rightarrow\:\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$=\mathrm{e}^{\mathrm{2x}} ×\left(−\frac{\mathrm{2}}{\mathrm{7}}\right)\mathrm{e}^{−\mathrm{7x}} \:+\:\mathrm{e}^{−\mathrm{5x}} ×\left(−\mathrm{2x}\right)\:=−\frac{\mathrm{2}}{\mathrm{7}}\:\mathrm{e}^{−\mathrm{7x}} \:−\mathrm{2x}\:\mathrm{e}^{−\mathrm{5x}} \:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$\mathrm{y}\:=\:\mathrm{ae}^{\mathrm{2x}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{5x}} \:−\frac{\mathrm{2}}{\mathrm{7}}\:\mathrm{e}^{−\mathrm{7x}} \:−\mathrm{2x}\:\mathrm{e}^{−\mathrm{5x}} \\ $$$$ \\ $$

Commented by Ar Brandon last updated on 10/Jul/20

What's the theory, Sir ? ��

Commented by Ar Brandon last updated on 10/Jul/20

I understand you may be so busy by now. Please reply whenever you feel it's OK to do so.��

Commented by mathmax by abdo last updated on 10/Jul/20

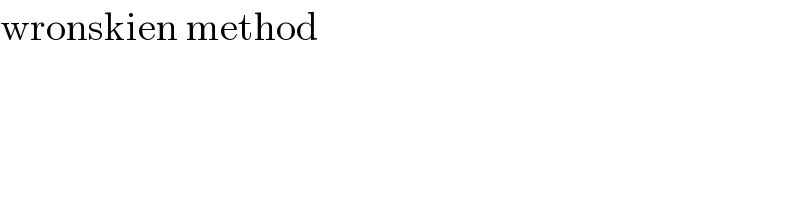
$$\mathrm{wronskien}\:\mathrm{method} \\ $$

Answered by Aziztisffola last updated on 10/Jul/20

Facebook Tweet Pin

Leave a Reply Cancel reply