Menu Close

y-3y-2y-1-1-e-x-

Tinku Tara 0 Comments
Pin




Question Number 118274 by bobhans last updated on 16/Oct/20
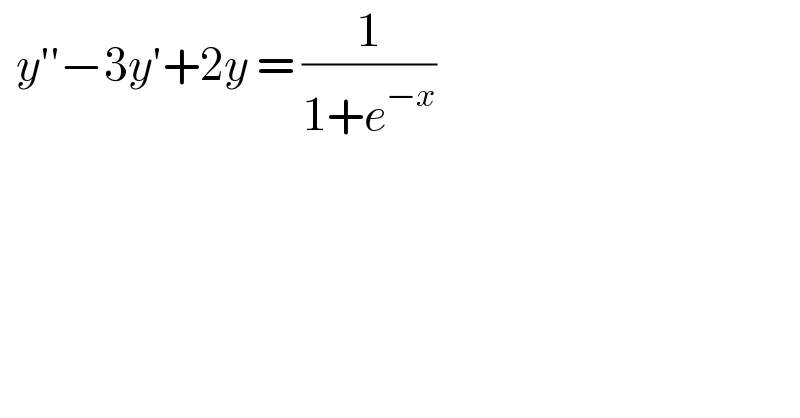
y′′−3y′+2y = (1/(1+e^(−x) ))
$$\:\:{y}''−\mathrm{3}{y}'+\mathrm{2}{y}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{e}^{−{x}} }\: \\ $$
Answered by mathmax by abdo last updated on 16/Oct/20
h→r^2 −3r+2=0 →Δ=9−8=1 ⇒r_1 =((3+1)/2)=2 and r_2 =((3−1)/2)=1 ⇒ y_h =ae^x +b e^(2x) =au_1 +bu_2 W(u_1 ,u_2 )= determinant (((e^x e^(2x) )),((e^x 2e^(2x) )))=2e^(3x) −e^(3x) =e^(3x) ≠o W_1 = determinant (((o e^(2x) )),(((1/(1+e^(−x) )) 2e^(2x) )))=−(e^(2x) /(1+e^(−x) )) W_2 = determinant (((e^x 0)),((e^x (1/(1+e^(−x) )))))=(e^x /(1+e^(−x) )) v_1 =∫ (W_1 /W)dx =−∫ (e^(2x) /((1+e^(−x) )e^(3x) ))dx =−∫ (e^(−x) /(1+e^(−x) ))dx =ln(1+e^(−x) ) v_2 =∫ (W_2 /W)dx =∫ (e^x /((1+e^(−x) )e^(3x) )) =∫ (e^(−2x) /(1+e^(−x) ))dx =∫ (dx/(e^(2x) (1+e^(−x) ))) =∫ (dx/(e^(2x) +e^x )) =_(e^x =t) ∫ (dt/(t(t^2 +t))) =∫ (dt/(t^2 (t+1))) F(t)=(1/(t^2 (t+1))) =(a/t)+(b/t^2 ) +(c/(t+1)) b=1 , c=1 lim_(t→+∞) tF(t) =0 =a+c ⇒a=−1 ⇒ F(t)=−(1/t) +(1/t^2 ) +(1/(t+1)) ⇒v_2 =−ln∣t∣−(1/t) +ln∣t+1∣ =−x −e^(−x) +ln(1+e^x ) ⇒y_p =u_1 v_1 +u_2 v_2 =e^x ln(1+e^(−x) ) +e^(2x) (−x−e^(−x) +ln(1+e^x )) =e^x ln(1+e^(−x) )−x e^(2x) −e^x +e^(2x) ln(1+e^x ) the genearal solution is y =y_h +y_p
$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{3r}+\mathrm{2}=\mathrm{0}\:\rightarrow\Delta=\mathrm{9}−\mathrm{8}=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} +\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{2e}^{\mathrm{3x}} −\mathrm{e}^{\mathrm{3x}} \:=\mathrm{e}^{\mathrm{3x}} \:\neq\mathrm{o} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\:\:\:\:\:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }}\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=−\int\:\:\:\:\frac{\mathrm{e}^{\mathrm{2x}} }{\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\mathrm{e}^{\mathrm{3x}} }\mathrm{dx}\:=−\int\:\:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\:\frac{\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\mathrm{e}^{\mathrm{3x}} }\:=\int\:\:\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=\int\:\:\:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{2x}} \left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{2x}} +\mathrm{e}^{\mathrm{x}} }\:=_{\mathrm{e}^{\mathrm{x}} =\mathrm{t}} \:\:\:\:\:\int\:\:\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\right)}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)}\:=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{b}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{t}+\mathrm{1}} \\ $$$$\mathrm{b}=\mathrm{1}\:\:,\:\:\mathrm{c}=\mathrm{1}\:\:\:\:\:\:\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{c}\:\Rightarrow\mathrm{a}=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=−\frac{\mathrm{1}}{\mathrm{t}}\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\:\Rightarrow\mathrm{v}_{\mathrm{2}} =−\mathrm{ln}\mid\mathrm{t}\mid−\frac{\mathrm{1}}{\mathrm{t}}\:+\mathrm{ln}\mid\mathrm{t}+\mathrm{1}\mid \\ $$$$=−\mathrm{x}\:−\mathrm{e}^{−\mathrm{x}} \:+\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$=\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\:\:+\mathrm{e}^{\mathrm{2x}} \left(−\mathrm{x}−\mathrm{e}^{−\mathrm{x}} +\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\right) \\ $$$$=\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{x}\:\mathrm{e}^{\mathrm{2x}} −\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{\mathrm{2x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\:\mathrm{the}\:\mathrm{genearal}\:\mathrm{solution} \\ $$$$\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$ \\ $$
Answered by bramlexs22 last updated on 16/Oct/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *