Menu Close

y-3y-2y-10sin-x-2cos-2x-

Tinku Tara 0 Comments
Pin




Question Number 87904 by john santu last updated on 07/Apr/20
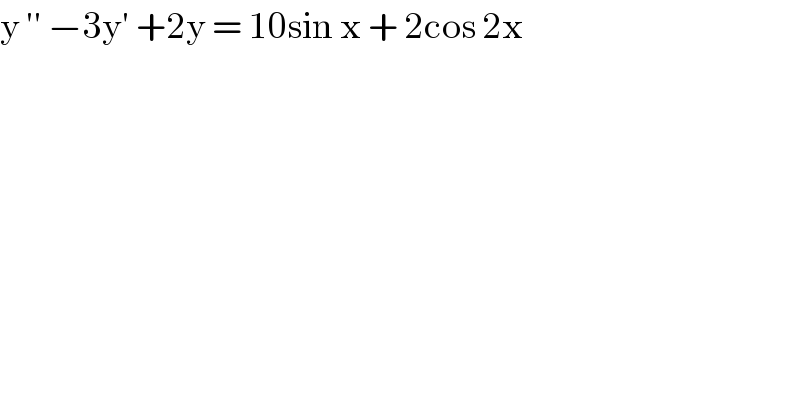
y ′′ −3y′ +2y = 10sin x + 2cos 2x
$$\mathrm{y}\:''\:−\mathrm{3y}'\:+\mathrm{2y}\:=\:\mathrm{10sin}\:\mathrm{x}\:+\:\mathrm{2cos}\:\mathrm{2x} \\ $$
Commented by niroj last updated on 07/Apr/20
y^(′′) −3y^′ +2y=10sin x+2cos 2x (D^2 −3D+2)y=10sin x+2cos2x A.E., m^2 −3m+2=0 (m−2)(m−1)=0 m=1,2 CF= C_1 e^x +C_2 e^(2x) PI= ((10sin x)/(D^2 −3D+2)) + ((2cos2x)/(D^2 −3D+2)) = ((10sin x)/(−1−3D+2)) + ((2cos2x)/(−4−4D+2)) = ((10sin x)/(−3D+1)) + ((2cos2x)/(−2−4D)) = ((−10sin x)/((3D−1)))− ((2cos2x)/(2(2D+1))) = ((−10(3D+1)sin x)/(9D^2 −1))− (((2D−1)cos2x)/(4D^2 −1)) = ((−10(3Dsin x+sin x))/(−9−1))− (((2Dcos2x−cos2x))/(−16−1)) = ((−10)/(−10))(3cos x+sinx)+(1/(17))(−4sin2x−cos2x) = 3cos x+sin x− (1/(17))(4sin x+cos2x) y=CF+PI y=C_1 e^x +C_2 e^(2x) + sin x+ 3cos x−(1/(17))(4 sin x + cos 2x)//.
$$\:\:\mathrm{y}^{''} −\mathrm{3y}^{'} +\mathrm{2y}=\mathrm{10sin}\:\mathrm{x}+\mathrm{2cos}\:\mathrm{2x} \\ $$$$\:\:\:\left(\mathrm{D}^{\mathrm{2}} −\mathrm{3D}+\mathrm{2}\right)\mathrm{y}=\mathrm{10sin}\:\mathrm{x}+\mathrm{2cos2x} \\ $$$$\:\:\:\:\mathrm{A}.\mathrm{E}.,\:\:\mathrm{m}^{\mathrm{2}} −\mathrm{3m}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{m}−\mathrm{2}\right)\left(\mathrm{m}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{m}=\mathrm{1},\mathrm{2} \\ $$$$\:\:\:\:\:\mathrm{CF}=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} \\ $$$$\:\:\mathrm{PI}=\:\frac{\mathrm{10sin}\:\mathrm{x}}{\mathrm{D}^{\mathrm{2}} −\mathrm{3D}+\mathrm{2}}\:+\:\frac{\mathrm{2cos2x}}{\mathrm{D}^{\mathrm{2}} −\mathrm{3D}+\mathrm{2}} \\ $$$$\:\:=\:\frac{\mathrm{10sin}\:\mathrm{x}}{−\mathrm{1}−\mathrm{3D}+\mathrm{2}}\:+\:\frac{\mathrm{2cos2x}}{−\mathrm{4}−\mathrm{4D}+\mathrm{2}} \\ $$$$\:\:\:=\:\frac{\mathrm{10sin}\:\mathrm{x}}{−\mathrm{3D}+\mathrm{1}}\:+\:\frac{\mathrm{2cos2x}}{−\mathrm{2}−\mathrm{4D}} \\ $$$$\:\:=\:\frac{−\mathrm{10sin}\:\mathrm{x}}{\left(\mathrm{3D}−\mathrm{1}\right)}−\:\frac{\mathrm{2cos2x}}{\mathrm{2}\left(\mathrm{2D}+\mathrm{1}\right)} \\ $$$$=\:\:\frac{−\mathrm{10}\left(\mathrm{3D}+\mathrm{1}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{9D}^{\mathrm{2}} −\mathrm{1}}−\:\frac{\left(\mathrm{2D}−\mathrm{1}\right)\mathrm{cos2x}}{\mathrm{4D}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\:\:\frac{−\mathrm{10}\left(\mathrm{3Dsin}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)}{−\mathrm{9}−\mathrm{1}}−\:\frac{\left(\mathrm{2Dcos2x}−\mathrm{cos2x}\right)}{−\mathrm{16}−\mathrm{1}} \\ $$$$=\:\frac{−\mathrm{10}}{−\mathrm{10}}\left(\mathrm{3cos}\:\mathrm{x}+\mathrm{sinx}\right)+\frac{\mathrm{1}}{\mathrm{17}}\left(−\mathrm{4sin2x}−\mathrm{cos2x}\right) \\ $$$$=\:\mathrm{3cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}−\:\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{4sin}\:\mathrm{x}+\mathrm{cos2x}\right) \\ $$$$\:\mathrm{y}=\mathrm{CF}+\mathrm{PI} \\ $$$$\:\mathrm{y}=\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} +\:\mathrm{sin}\:\mathrm{x}+\:\mathrm{3cos}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{4}\:\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{cos}\:\mathrm{2x}\right)//. \\ $$$$ \\ $$
Commented by john santu last updated on 07/Apr/20
thank you all
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all} \\ $$
Answered by Joel578 last updated on 07/Apr/20
• Homogeneous solution Ch. eq: λ^2 − 3λ + 2 = 0 → λ_1 = 1, λ_2 = 2 y_h (x) = C_1 e^x + C_2 e^(2x) • Particular solution y_p (x) = A sin x + B cos x + M sin 2x + N cos 2x y_p ′(x) = A cos x − B sin x + 2M cos 2x − 2N sin 2x y_p ^(′′) (x) = −A sin x − B cos x − 4M sin 2x − 4N cos 2x y_p ^(′′) − 3y_p ^′ + 2y_p = 10sin x + 2cos 2x ⇒ [A+3B]sin x + [−3A+B]cos x + [−2M+6N]sin 2x + [−6M−2N]cos 2x = 10sin x + 2cos 2x Comparing coeff. in LHS and RHS { (( A + 3B = 10)),((−3A + B = 0)) :} and { ((−2M + 6N = 0)),((−6M − 2N = 2)) :} ⇒ A = 1, B = 3, M = −(3/(10)), N = −(1/(10)) ⇒ y_p (x) = sin x + 3cos x − (3/(10))sin 2x − (1/(10))cos 2x ∴ y(x) = y_h (x) + y_p (x)
$$\bullet\:\mathrm{Homogeneous}\:\mathrm{solution} \\ $$$$\mathrm{Ch}.\:\mathrm{eq}:\:\lambda^{\mathrm{2}} \:−\:\mathrm{3}\lambda\:+\:\mathrm{2}\:=\:\mathrm{0}\:\rightarrow\:\lambda_{\mathrm{1}} \:=\:\mathrm{1},\:\lambda_{\mathrm{2}} \:=\:\mathrm{2} \\ $$$${y}_{{h}} \left({x}\right)\:=\:{C}_{\mathrm{1}} {e}^{{x}} \:+\:{C}_{\mathrm{2}} {e}^{\mathrm{2}{x}} \\ $$$$ \\ $$$$\bullet\:\mathrm{Particular}\:\mathrm{solution} \\ $$$${y}_{{p}} \left({x}\right)\:\:=\:{A}\:\mathrm{sin}\:{x}\:+\:{B}\:\mathrm{cos}\:{x}\:+\:{M}\:\mathrm{sin}\:\mathrm{2}{x}\:+\:{N}\:\mathrm{cos}\:\mathrm{2}{x} \\ $$$${y}_{{p}} '\left({x}\right)\:=\:{A}\:\mathrm{cos}\:{x}\:−\:{B}\:\mathrm{sin}\:{x}\:+\:\mathrm{2}{M}\:\mathrm{cos}\:\mathrm{2}{x}\:−\:\mathrm{2}{N}\:\mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}_{{p}} ^{''} \left({x}\right)\:\:=\:−{A}\:\mathrm{sin}\:{x}\:−\:{B}\:\mathrm{cos}\:{x}\:−\:\mathrm{4}{M}\:\mathrm{sin}\:\mathrm{2}{x}\:−\:\mathrm{4}{N}\:\mathrm{cos}\:\mathrm{2}{x} \\ $$$$ \\ $$$${y}_{{p}} ^{''} \:−\:\mathrm{3}{y}_{{p}} ^{'} \:+\:\mathrm{2}{y}_{{p}} \:=\:\mathrm{10sin}\:{x}\:+\:\mathrm{2cos}\:\mathrm{2}{x} \\ $$$$\Rightarrow\:\left[{A}+\mathrm{3}{B}\right]\mathrm{sin}\:{x}\:+\:\left[−\mathrm{3}{A}+{B}\right]\mathrm{cos}\:{x}\:+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left[−\mathrm{2}{M}+\mathrm{6}{N}\right]\mathrm{sin}\:\mathrm{2}{x}\:+\:\left[−\mathrm{6}{M}−\mathrm{2}{N}\right]\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{10sin}\:{x}\:+\:\mathrm{2cos}\:\mathrm{2}{x} \\ $$$$\mathrm{Comparing}\:\mathrm{coeff}.\:\mathrm{in}\:\mathrm{LHS}\:\mathrm{and}\:\mathrm{RHS} \\ $$$$\begin{cases}{\:\:\:\:\:\:\:{A}\:+\:\mathrm{3}{B}\:=\:\mathrm{10}}\\{−\mathrm{3}{A}\:+\:\:\:{B}\:=\:\:\:\:\mathrm{0}}\end{cases}\:\:\:\:\mathrm{and}\:\:\:\begin{cases}{−\mathrm{2}{M}\:+\:\mathrm{6}{N}\:=\:\mathrm{0}}\\{−\mathrm{6}{M}\:−\:\mathrm{2}{N}\:=\:\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:{A}\:=\:\mathrm{1},\:{B}\:=\:\mathrm{3},\:{M}\:=\:−\frac{\mathrm{3}}{\mathrm{10}},\:{N}\:=\:−\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\Rightarrow\:{y}_{{p}} \left({x}\right)\:=\:\mathrm{sin}\:{x}\:+\:\mathrm{3cos}\:{x}\:−\:\frac{\mathrm{3}}{\mathrm{10}}\mathrm{sin}\:\mathrm{2}{x}\:−\:\frac{\mathrm{1}}{\mathrm{10}}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$ \\ $$$$\therefore\:{y}\left({x}\right)\:=\:{y}_{{h}} \left({x}\right)\:+\:{y}_{{p}} \left({x}\right) \\ $$
Answered by TANMAY PANACEA. last updated on 07/Apr/20
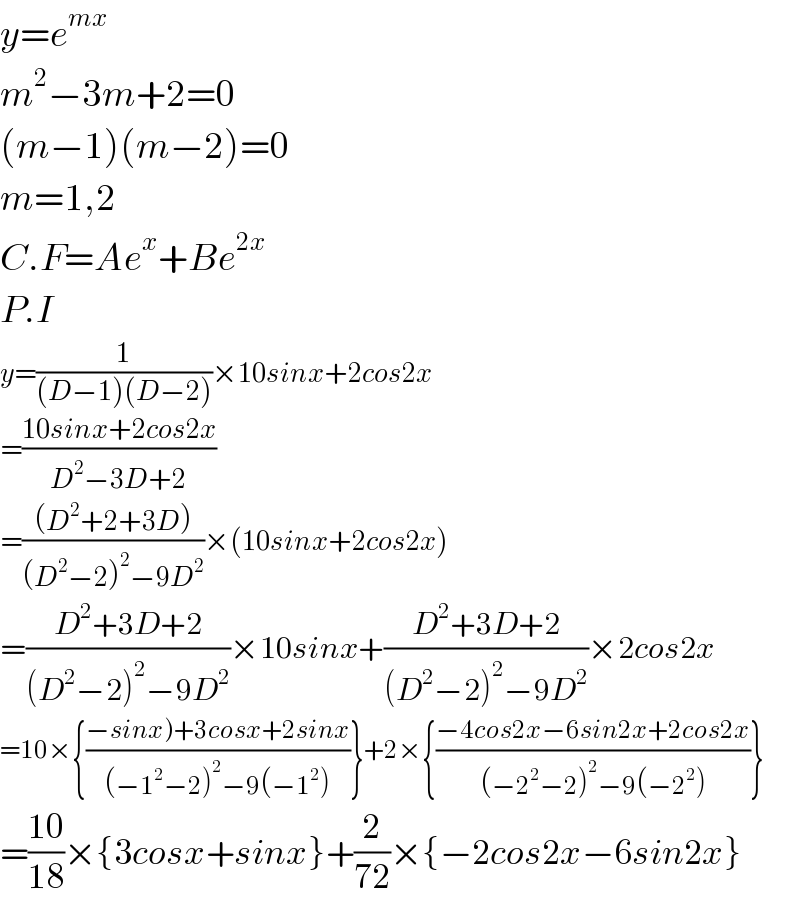
y=e^(mx) m^2 −3m+2=0 (m−1)(m−2)=0 m=1,2 C.F=Ae^x +Be^(2x) P.I y=(1/((D−1)(D−2)))×10sinx+2cos2x =((10sinx+2cos2x)/(D^2 −3D+2)) =(((D^2 +2+3D))/((D^2 −2)^2 −9D^2 ))×(10sinx+2cos2x) =((D^2 +3D+2)/((D^2 −2)^2 −9D^2 ))×10sinx+((D^2 +3D+2)/((D^2 −2)^2 −9D^2 ))×2cos2x =10×{((−sinx)+3cosx+2sinx)/((−1^2 −2)^2 −9(−1^2 )))}+2×{((−4cos2x−6sin2x+2cos2x)/((−2^2 −2)^2 −9(−2^2 )))} =((10)/(18))×{3cosx+sinx}+(2/(72))×{−2cos2x−6sin2x}
$${y}={e}^{{mx}} \\ $$$${m}^{\mathrm{2}} −\mathrm{3}{m}+\mathrm{2}=\mathrm{0} \\ $$$$\left({m}−\mathrm{1}\right)\left({m}−\mathrm{2}\right)=\mathrm{0} \\ $$$${m}=\mathrm{1},\mathrm{2} \\ $$$${C}.{F}={Ae}^{{x}} +{Be}^{\mathrm{2}{x}} \\ $$$${P}.{I} \\ $$$${y}=\frac{\mathrm{1}}{\left({D}−\mathrm{1}\right)\left({D}−\mathrm{2}\right)}×\mathrm{10}{sinx}+\mathrm{2}{cos}\mathrm{2}{x} \\ $$$$=\frac{\mathrm{10}{sinx}+\mathrm{2}{cos}\mathrm{2}{x}}{{D}^{\mathrm{2}} −\mathrm{3}{D}+\mathrm{2}} \\ $$$$=\frac{\left({D}^{\mathrm{2}} +\mathrm{2}+\mathrm{3}{D}\right)}{\left({D}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}{D}^{\mathrm{2}} }×\left(\mathrm{10}{sinx}+\mathrm{2}{cos}\mathrm{2}{x}\right) \\ $$$$=\frac{{D}^{\mathrm{2}} +\mathrm{3}{D}+\mathrm{2}}{\left({D}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}{D}^{\mathrm{2}} }×\mathrm{10}{sinx}+\frac{{D}^{\mathrm{2}} +\mathrm{3}{D}+\mathrm{2}}{\left({D}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}{D}^{\mathrm{2}} }×\mathrm{2}{cos}\mathrm{2}{x} \\ $$$$=\mathrm{10}×\left\{\frac{\left.−{sinx}\right)+\mathrm{3}{cosx}+\mathrm{2}{sinx}}{\left(−\mathrm{1}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}\left(−\mathrm{1}^{\mathrm{2}} \right)}\right\}+\mathrm{2}×\left\{\frac{−\mathrm{4}{cos}\mathrm{2}{x}−\mathrm{6}{sin}\mathrm{2}{x}+\mathrm{2}{cos}\mathrm{2}{x}}{\left(−\mathrm{2}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{9}\left(−\mathrm{2}^{\mathrm{2}} \right)}\right\} \\ $$$$=\frac{\mathrm{10}}{\mathrm{18}}×\left\{\mathrm{3}{cosx}+{sinx}\right\}+\frac{\mathrm{2}}{\mathrm{72}}×\left\{−\mathrm{2}{cos}\mathrm{2}{x}−\mathrm{6}{sin}\mathrm{2}{x}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *