Menu Close

y-3y-2y-xsin-x-

Tinku Tara 0 Comments
Pin




Question Number 114225 by mohammad17 last updated on 17/Sep/20
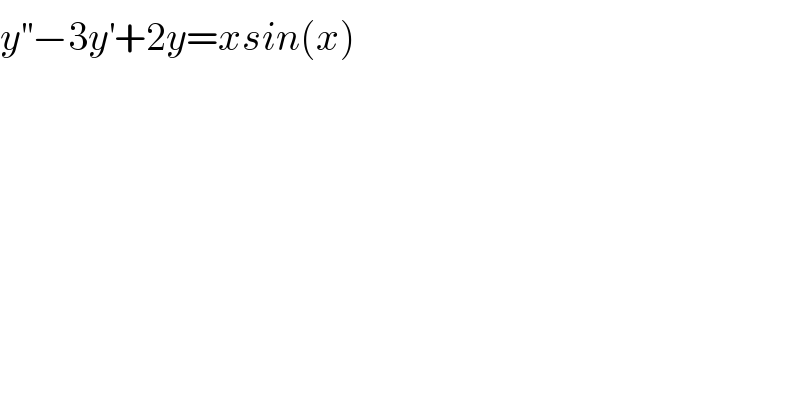
y^(′′) −3y^′ +2y=xsin(x)
$${y}^{''} −\mathrm{3}{y}^{'} +\mathrm{2}{y}={xsin}\left({x}\right) \\ $$
Answered by mathmax by abdo last updated on 18/Sep/20
h→r^2 −3r+2=0→Δ =9−8=1 ⇒r_1 =((3+1)/2)=2 and r_2 =((3−1)/2)=1 ⇒ y_h =ae^(2x) +be^x =au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((e^(2x) e^x )),((2e^(2x) e^x )))=e^(3x) −2e^(3x) =−e^(3x) ≠0 W_1 = determinant (((0 e^x )),((xsinx e^x )))=−xe^x sinx W_2 = determinant (((e^(2x) 0)),((2e^(2x) xsinx)))=xe^(2x) sinx V_1 =∫ (W_1 /W)dx =∫ ((−xe^x sinx)/(−e^(3x) )) dx =∫ x e^(−2x) sinx dx =Im(∫ x e^(−2x+ix) dx) but ∫ x e^((−2+i)x) dx =(x/(−2+i)) e^((−2+i)x) −∫ (1/(−2+i)) e^((−2+i)x) dx =−x((2+i)/5) e^((−2+i)x) +(1/(2−i))×(1/(−2+i)) e^((−2+i)x) =−(x/5)(2+i)e^((−2+i)x) −(((2+i)^2 )/((5)^2 )) e^((−2+i)x) ={−(x/5)(2+i)−((3+4i)/(25))}e^(−2x) (cosx +isinx) =((−5x(2+i)−3−4i)/(25)) e^(−2x) (cosx +isinx) =((−10x−5ix−3−4i)/(25)) e^(−2x) (cosx +isinx)=.... V_2 =∫ (W_2 /W)dx =∫ ((xe^(2x) sinx)/(−e^(3x) )) dx =−∫ x e^(−x) sinx dx =−Im(∫ x e^(−x+ix) dx) but ∫ x e^((−1+i)x) dx =(x/(−1+i)) e^((−1+i)x) +∫ (1/(−1+i)) e^((−1+i)x) dx =e^(−x) (cosx +isinx){((−x)/(1−i))−(1/(1−i))} =e^(−x) (cosx +sinx){((−x(1+i))/2)−((1+i)/2)} =.... ⇒y_p =u_1 v_1 +u_2 v_2 =e^(2x) ∫ xe^(−2x) sinx dx −e^x ∫ x e^(−x) sinx dx the general solution is y =y_h +y_p
$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{3r}+\mathrm{2}=\mathrm{0}\rightarrow\Delta\:=\mathrm{9}−\mathrm{8}=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{2x}} \:+\mathrm{be}^{\mathrm{x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=\mathrm{e}^{\mathrm{3x}} −\mathrm{2e}^{\mathrm{3x}} \:=−\mathrm{e}^{\mathrm{3x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\mathrm{xsinx}\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=−\mathrm{xe}^{\mathrm{x}} \:\mathrm{sinx} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\mathrm{xsinx}}\end{vmatrix}=\mathrm{xe}^{\mathrm{2x}} \:\mathrm{sinx} \\ $$$$\mathrm{V}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{xe}^{\mathrm{x}} \:\mathrm{sinx}}{−\mathrm{e}^{\mathrm{3x}} }\:\mathrm{dx}\:=\int\:\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{sinx}\:\mathrm{dx} \\ $$$$=\mathrm{Im}\left(\int\:\:\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{but}\:\int\:\mathrm{x}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx}\:=\frac{\mathrm{x}}{−\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \\ $$$$−\int\:\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx}\:=−\mathrm{x}\frac{\mathrm{2}+\mathrm{i}}{\mathrm{5}}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{i}}×\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \\ $$$$=−\frac{\mathrm{x}}{\mathrm{5}}\left(\mathrm{2}+\mathrm{i}\right)\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:−\frac{\left(\mathrm{2}+\mathrm{i}\right)^{\mathrm{2}} \:}{\left(\mathrm{5}\right)^{\mathrm{2}} }\:\mathrm{e}^{\left(−\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \\ $$$$=\left\{−\frac{\mathrm{x}}{\mathrm{5}}\left(\mathrm{2}+\mathrm{i}\right)−\frac{\mathrm{3}+\mathrm{4i}}{\mathrm{25}}\right\}\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right) \\ $$$$=\frac{−\mathrm{5x}\left(\mathrm{2}+\mathrm{i}\right)−\mathrm{3}−\mathrm{4i}}{\mathrm{25}}\:\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right) \\ $$$$=\frac{−\mathrm{10x}−\mathrm{5ix}−\mathrm{3}−\mathrm{4i}}{\mathrm{25}}\:\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right)=…. \\ $$$$\mathrm{V}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{xe}^{\mathrm{2x}} \:\mathrm{sinx}}{−\mathrm{e}^{\mathrm{3x}} }\:\mathrm{dx}\:=−\int\:\mathrm{x}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{sinx}\:\mathrm{dx} \\ $$$$=−\mathrm{Im}\left(\int\:\mathrm{x}\:\mathrm{e}^{−\mathrm{x}+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{but}\:\int\:\mathrm{x}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\mathrm{x}}{−\mathrm{1}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:+\int\:\frac{\mathrm{1}}{−\mathrm{1}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right)\left\{\frac{−\mathrm{x}}{\mathrm{1}−\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{i}}\right\}\: \\ $$$$=\mathrm{e}^{−\mathrm{x}} \left(\mathrm{cosx}\:+\mathrm{sinx}\right)\left\{\frac{−\mathrm{x}\left(\mathrm{1}+\mathrm{i}\right)}{\mathrm{2}}−\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\right\}\:=…. \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{e}^{\mathrm{2x}} \:\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{sinx}\:\mathrm{dx}\:−\mathrm{e}^{\mathrm{x}} \:\int\:\mathrm{x}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{sinx}\:\mathrm{dx} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *