Question Number 101419 by bemath last updated on 02/Jul/20
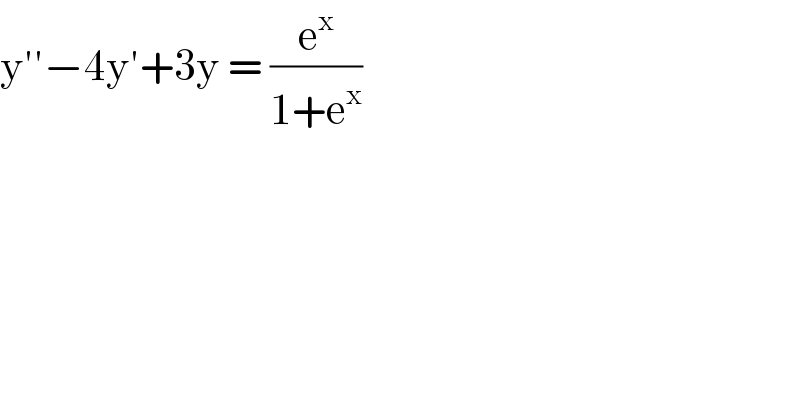
$$\mathrm{y}''−\mathrm{4y}'+\mathrm{3y}\:=\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} } \\ $$
Answered by john santu last updated on 02/Jul/20
![AE: λ^2 −4λ+3 = 0 (λ−1)(λ−3)=0 y_h = C_1 e^x + C_2 e^(3x ) →y_1 = e^x ∧y_2 = e^(3x) W = determinant (((y_1 y_2 )),((y_1 ^′ y_2 ′)))= determinant (((e^x e^(3x) )),((e^x 3e^(3x) ))) W= 3e^(4x) −e^(4x) = 2e^(3x) particular integral =−(e^x /2)∫ (e^x /(e^x (1+e^x ))) dx + (e^(3x) /2)∫ (e^x /e^(4x) ) .(e^x /((1+e^x ))) dx =−(e^x /2)∫ (dx/(1+e^x )) + (e^(3x) /2)∫ (dx/(e^(2x) (1+e^x ))) I_1 = ∫ (dx/(1+e^x )) [ set e^x = z , dx = (dz/e^x )] I_1 = ∫ (dz/(z(1+z))) = ∫ (dz/z)−∫ (dz/(1+z)) I_1 = ln((z/(1+z))) = ln ((e^x /(1+e^x ))) I_2 = ∫(dx/(e^(2x) (1+e^x ))) [ set e^x = p ] I_2 = ∫ (dp/(p^3 (1+p))) = ∫ (dp/p)−∫ (dp/p^2 ) +∫ (dp/p^3 )−∫ (dp/((1+p))) I_2 = ln(p)+(1/p)−(1/(2p^2 ))−ln(1+p) I_2 = ln((e^x /(1+e^x ))) +(1/e^x ) −(1/(2e^(2x) )) particular solution y_p = −(e^x /2)ln((e^x /(1+e^x )))+(e^(3x) /2)((1/e^x )−(1/(2e^(2x) )) + ln((e^x /(1+e^x )))) Generall solution y_g = y_h + y_p](https://www.tinkutara.com/question/Q101421.png)
$$\mathrm{AE}:\:\lambda^{\mathrm{2}} −\mathrm{4}\lambda+\mathrm{3}\:=\:\mathrm{0} \\ $$$$\left(\lambda−\mathrm{1}\right)\left(\lambda−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:+\:\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{3x}\:} \\ $$$$\rightarrow\mathrm{y}_{\mathrm{1}} =\:\mathrm{e}^{\mathrm{x}} \:\wedge\mathrm{y}_{\mathrm{2}} =\:\mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{W}\:=\:\begin{vmatrix}{\mathrm{y}_{\mathrm{1}} \:\:\:\:\mathrm{y}_{\mathrm{2}} }\\{\mathrm{y}_{\mathrm{1}} ^{'} \:\:\:\:\mathrm{y}_{\mathrm{2}} '}\end{vmatrix}=\:\begin{vmatrix}{{e}^{{x}} \:\:\:\:\:{e}^{\mathrm{3}{x}} }\\{{e}^{{x}} \:\:\:\:\mathrm{3}{e}^{\mathrm{3}{x}} }\end{vmatrix} \\ $$$${W}=\:\mathrm{3e}^{\mathrm{4x}} −\mathrm{e}^{\mathrm{4x}} \:=\:\mathrm{2e}^{\mathrm{3x}} \: \\ $$$$\mathrm{particular}\:\mathrm{integral}\: \\ $$$$=−\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\int\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)}\:\mathrm{dx}\:+\:\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{2}}\int\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{4x}} }\:.\frac{\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:+\:\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{2}}\int\:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{2x}} \left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\int\:\frac{{dx}}{\mathrm{1}+{e}^{{x}} }\:\:\left[\:{set}\:{e}^{{x}} \:=\:{z}\:,\:{dx}\:=\:\frac{{dz}}{{e}^{{x}} }\right] \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\int\:\frac{{dz}}{{z}\left(\mathrm{1}+{z}\right)}\:=\:\int\:\frac{{dz}}{{z}}−\int\:\frac{{dz}}{\mathrm{1}+{z}} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\mathrm{ln}\left(\frac{{z}}{\mathrm{1}+{z}}\right)\:=\:\mathrm{ln}\:\left(\frac{{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right) \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int\frac{{dx}}{{e}^{\mathrm{2}{x}} \left(\mathrm{1}+{e}^{{x}} \right)}\:\:\left[\:{set}\:{e}^{{x}} \:=\:{p}\:\right]\: \\ $$$$\mathrm{I}_{\mathrm{2}} \:=\:\int\:\frac{{dp}}{{p}^{\mathrm{3}} \left(\mathrm{1}+{p}\right)}\:=\:\int\:\frac{{dp}}{{p}}−\int\:\frac{{dp}}{{p}^{\mathrm{2}} }\:+\int\:\frac{{dp}}{{p}^{\mathrm{3}} }−\int\:\frac{{dp}}{\left(\mathrm{1}+{p}\right)} \\ $$$$\mathrm{I}_{\mathrm{2}} \:=\:\mathrm{ln}\left({p}\right)+\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} }−\mathrm{ln}\left(\mathrm{1}+{p}\right) \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\mathrm{ln}\left(\frac{\mathrm{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right)\:+\frac{\mathrm{1}}{{e}^{{x}} }\:−\frac{\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}{x}} } \\ $$$$\mathrm{particular}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{p}} =\:−\frac{{e}^{{x}} }{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right)+\frac{{e}^{\mathrm{3}{x}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{{e}^{{x}} }−\frac{\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}{x}} }\:+\:\mathrm{ln}\left(\frac{{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right)\right) \\ $$$$\mathcal{G}\mathrm{enerall}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{g}} \:=\:\mathrm{y}_{\mathrm{h}} \:+\:\mathrm{y}_{\mathrm{p}} \: \\ $$
Answered by mathmax by abdo last updated on 02/Jul/20

$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} −\mathrm{4y}^{'} \:+\mathrm{3y}\:=\mathrm{0}\:\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}\:+\mathrm{3}=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{4}−\mathrm{3}\:=\mathrm{1}\:\Rightarrow\:\mathrm{r}_{\mathrm{1}} =\mathrm{2}+\mathrm{1}\:=\mathrm{3}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{3x}} \:+\mathrm{be}^{\mathrm{x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{3x}\:\:\:\:\:\:} \:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\mathrm{3e}^{\mathrm{3x}} \:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=\mathrm{e}^{\mathrm{4x}} −\mathrm{3e}^{\mathrm{4x}} \:=−\mathrm{2e}^{\mathrm{4x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=−\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} } \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{3e}^{\mathrm{3x}} \:\:\:\:\:\:\:\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }}\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{4x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} } \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\:−\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }×\frac{\mathrm{1}}{−\mathrm{2e}^{\mathrm{4x}} }\:=\int\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{2}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)}\:\:=_{\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}} \:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}\right)}×\frac{\mathrm{dt}}{\mathrm{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{t}\right)}\:\:\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{1}\right)\mathrm{t}^{\mathrm{3}} } \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{t}}\:+\frac{\mathrm{c}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{d}}{\mathrm{t}^{\mathrm{3}} } \\ $$$$\mathrm{a}\:=−\mathrm{1}\:\:\:\:,\mathrm{d}\:=\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{t}}\:+\frac{\mathrm{c}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} } \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=−\mathrm{1}+\mathrm{b}\:\Rightarrow\mathrm{b}=\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{t}}\:+\frac{\mathrm{c}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} } \\ $$$$\mathrm{F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{1}+\mathrm{c}\:+\mathrm{1}\:=\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\:\Rightarrow\mathrm{v}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{ln}\mid\mathrm{t}+\mathrm{1}\mid+\mathrm{ln}\mid\mathrm{t}\mid+\frac{\mathrm{1}}{\mathrm{t}}\:−\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)\:+\mathrm{e}^{−\mathrm{x}} \:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\mathrm{4x}} }{\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\left(−\mathrm{2e}^{\mathrm{4x}} \right)}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:=_{\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}} \:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mid\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right) \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{e}^{\mathrm{3x}} ×\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)+\mathrm{e}^{−\mathrm{x}} \:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \right\} \\ $$$$+\mathrm{e}^{\mathrm{x}} ×\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{e}^{\mathrm{3x}} \mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}\:} −\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{e}^{\mathrm{x}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{3x}} −\mathrm{e}^{\mathrm{x}} \right)\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\right)+\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{2}}−\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{4}} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
