Menu Close

y-4y-4y-e-2x-x-2-

Tinku Tara 0 Comments
Pin




Question Number 103203 by bobhans last updated on 13/Jul/20
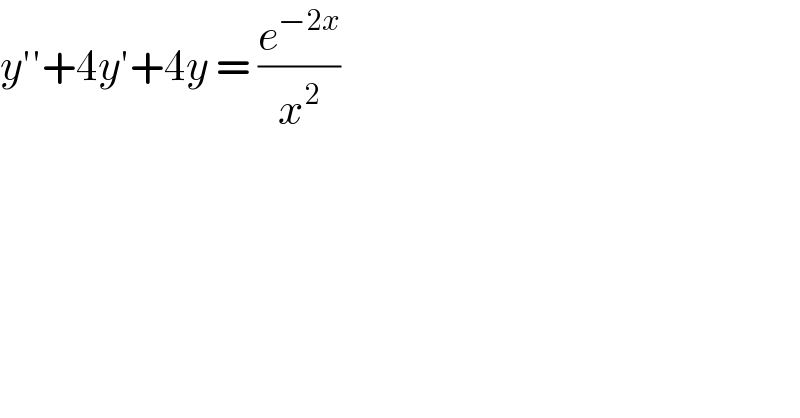
y′′+4y′+4y = (e^(−2x) /x^2 )
$${y}''+\mathrm{4}{y}'+\mathrm{4}{y}\:=\:\frac{{e}^{−\mathrm{2}{x}} }{{x}^{\mathrm{2}} }\: \\ $$
Answered by bramlex last updated on 14/Jul/20
characteristic eq χ^2 +4χ+4 = 0 ; (χ+2)^2 =0 y_h = C_1 e^(−2x) +C_2 xe^(−2x) now we apply reduction of order set y = e^(−2x) .z , substituting this into the original differential equation yields e^(−2x) (z′′−4z′+4z)+e^(−2x) (z′−2z) +4z e^(−2x) = (e^(−2x) /x^2 ) . which simplifies to z′′ = (1/x^2 ) intrgrating this twice succession yields z = −ln∣x∣ +C_1 x+C_2 hence a general solution is given by y = e^(−2x) {−ln∣x∣+C_2 x+C_1 } y = C_1 e^(−2x) + C_2 x e^(−2x) −e^(−2x) ln∣x∣ □
$$\mathrm{characteristic}\:\mathrm{eq}\: \\ $$$$\chi^{\mathrm{2}} +\mathrm{4}\chi+\mathrm{4}\:=\:\mathrm{0}\:;\:\left(\chi+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{h}} =\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} +\mathrm{C}_{\mathrm{2}} \mathrm{xe}^{−\mathrm{2x}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{apply}\:\mathrm{reduction}\:\mathrm{of}\:\mathrm{order} \\ $$$$\mathrm{set}\:\mathrm{y}\:=\:\mathrm{e}^{−\mathrm{2x}} .\mathrm{z}\:,\:\mathrm{substituting}\:\mathrm{this} \\ $$$$\mathrm{into}\:\mathrm{the}\:\mathrm{original}\:\mathrm{differential} \\ $$$$\mathrm{equation}\:\mathrm{yields}\: \\ $$$$\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{z}''−\mathrm{4z}'+\mathrm{4z}\right)+\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{z}'−\mathrm{2z}\right) \\ $$$$+\mathrm{4z}\:\mathrm{e}^{−\mathrm{2x}} \:=\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}^{\mathrm{2}} }\:.\:\mathrm{which} \\ $$$$\mathrm{simplifies}\:\mathrm{to}\:\mathrm{z}''\:=\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{intrgrating}\:\mathrm{this}\:\mathrm{twice}\:\mathrm{succession} \\ $$$$\mathrm{yields}\:\mathrm{z}\:=\:−\mathrm{ln}\mid\mathrm{x}\mid\:+\mathrm{C}_{\mathrm{1}} \mathrm{x}+\mathrm{C}_{\mathrm{2}} \\ $$$$\mathrm{hence}\:\mathrm{a}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{by}\:\mathrm{y}\:=\:\mathrm{e}^{−\mathrm{2x}} \left\{−\mathrm{ln}\mid\mathrm{x}\mid+\mathrm{C}_{\mathrm{2}} \mathrm{x}+\mathrm{C}_{\mathrm{1}} \right\}\: \\ $$$$\mathrm{y}\:=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} +\:\mathrm{C}_{\mathrm{2}} \mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} −\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\mid\mathrm{x}\mid\:\square \\ $$
Commented by bobhans last updated on 13/Jul/20
cooll....
Answered by mathmax by abdo last updated on 13/Jul/20
y^(′′) +4y^′ +4y =(e^(−2x) /x^2 ) (he)→y^(′′) +4y^′ +4y =0 →r^2 +4r +4 =0 ⇒(r+2)^2 =0 ⇒r =−2 ⇒y_h =(ax+b)e^(−2x) =axe^(−2x) +be^(−2x) =au_(1 ) +bu_2 W(u_(1 ,) u_2 ) = determinant (((xe^(−2x) e^(−2x) )),(((1−2x)e^(−2x) −2e^(−2x) )))=−2x e^(−2x) +(2x−1)e^(−2x) =−e^(−2x ) ≠0 W_1 = determinant (((o e^(−2x) )),(((e^(−2x) /x^2 ) −2e^(−2x) )))=−(e^(−4x) /x^2 ) W_2 = determinant (((xe^(−2x) 0)),(((1−2x)e^(−2x) (e^(−2x) /x^2 ))))=(e^(−4x) /x) v_1 =∫ (w_1 /w)dx =∫ (e^(−4x) /(x^2 e^(−2x) )) dx = ∫ (e^(−2x) /x^2 ) dx v_2 =∫ (w_2 /w) dx =−∫ (e^(−4x) /(x e^(−2x) ))dx =−∫ (e^(−2x) /x)dx ⇒ y_p =u_1 v_1 +u_2 v_2 =xe^(−2x) ∫^x (e^(−2t) /t)dt −e^(−2x ) ∫^x (e^(−2t) /t) dt y =y_h +y_p
$$\mathrm{y}^{''} \:+\mathrm{4y}^{'} \:+\mathrm{4y}\:=\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} \:+\mathrm{4y}^{'} \:+\mathrm{4y}\:=\mathrm{0}\:\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{4r}\:+\mathrm{4}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{r}+\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{r}\:=−\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{e}^{−\mathrm{2x}} \:=\mathrm{axe}^{−\mathrm{2x}} \:+\mathrm{be}^{−\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}\:} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}\:,} \mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{xe}^{−\mathrm{2x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\left(\mathrm{1}−\mathrm{2x}\right)\mathrm{e}^{−\mathrm{2x}} \:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{2x}\:\mathrm{e}^{−\mathrm{2x}} +\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:=−\mathrm{e}^{−\mathrm{2x}\:} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} }\\{\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:−\mathrm{2e}^{−\mathrm{2x}} }\end{vmatrix}=−\frac{\mathrm{e}^{−\mathrm{4x}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{xe}^{−\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{1}−\mathrm{2x}\right)\mathrm{e}^{−\mathrm{2x}} \:\:\:\:\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}^{\mathrm{2}} }}\end{vmatrix}=\frac{\mathrm{e}^{−\mathrm{4x}} }{\mathrm{x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{−\mathrm{4x}} }{\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2x}} }\:\mathrm{dx}\:=\:\int\:\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\:\mathrm{dx}\:=−\int\:\frac{\mathrm{e}^{−\mathrm{4x}} }{\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx}\:=−\int\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{x}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{xe}^{−\mathrm{2x}} \:\int^{\mathrm{x}} \:\frac{\mathrm{e}^{−\mathrm{2t}} }{\mathrm{t}}\mathrm{dt}\:\:−\mathrm{e}^{−\mathrm{2x}\:} \:\int^{\mathrm{x}} \:\:\frac{\mathrm{e}^{−\mathrm{2t}} }{\mathrm{t}}\:\mathrm{dt} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *