Question Number 91848 by jagoll last updated on 03/May/20
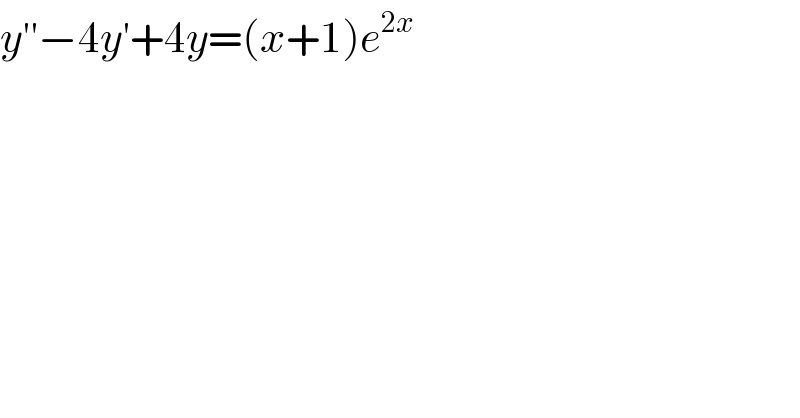
$${y}^{''} −\mathrm{4}{y}^{'} +\mathrm{4}{y}=\left({x}+\mathrm{1}\right){e}^{\mathrm{2}{x}} \\ $$$$ \\ $$
Commented by john santu last updated on 03/May/20

$${complementary}\:{solution} \\ $$$${m}^{\mathrm{2}} −\mathrm{4}{m}+\mathrm{4}=\mathrm{0} \\ $$$${m}_{\mathrm{1},\mathrm{2}} \:=\:\mathrm{2}\:\Rightarrow{y}_{{c}} \:=\:{A}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{A}_{\mathrm{2}} {e}^{\mathrm{2}{x}} \\ $$$${particular}\:{integral} \\ $$$${y}_{{p}} =\:\left({B}_{\mathrm{1}} {x}^{\mathrm{3}} +{B}_{\mathrm{2}} {x}^{\mathrm{2}} \right){e}^{\mathrm{2}{x}} \\ $$$${y}_{{p}} ^{'} \:=\:\left(\mathrm{3}{B}_{\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{2}{B}_{\mathrm{2}} {x}\right){e}^{\mathrm{2}{x}} \:+\mathrm{2}\left({B}_{\mathrm{1}} {x}^{\mathrm{3}} +{B}_{\mathrm{2}} {x}^{\mathrm{2}} \right){e}^{\mathrm{2}{x}} \\ $$$${y}_{{p}} ''\:=\:\left(\mathrm{6}{B}_{\mathrm{1}} {x}+\mathrm{2}{B}_{\mathrm{2}} \right){e}^{\mathrm{2}{x}} +\mathrm{2}\left(\mathrm{3}{B}_{\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{2}{B}_{\mathrm{2}} {x}\right){e}^{\mathrm{2}{x}} \\ $$$$\mathrm{2}\left(\mathrm{3}{B}_{\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{2}{B}_{\mathrm{2}} {x}\right){e}^{\mathrm{2}{x}} +\mathrm{4}\left({B}_{\mathrm{1}} {x}^{\mathrm{3}} +{B}_{\mathrm{2}} {x}^{\mathrm{2}} \right){e}^{\mathrm{2}{x}} \\ $$$${comparing}\:{coeff}\: \\ $$$${B}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}}\:;\:{B}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\therefore\:{y}=\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} \right){e}^{\mathrm{2}{x}} +\left(\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right){e}^{\mathrm{2}{x}} \\ $$
