y-4y-5y-1-8cos-x-e-2x-

Question Number 88492 by jagoll last updated on 11/Apr/20

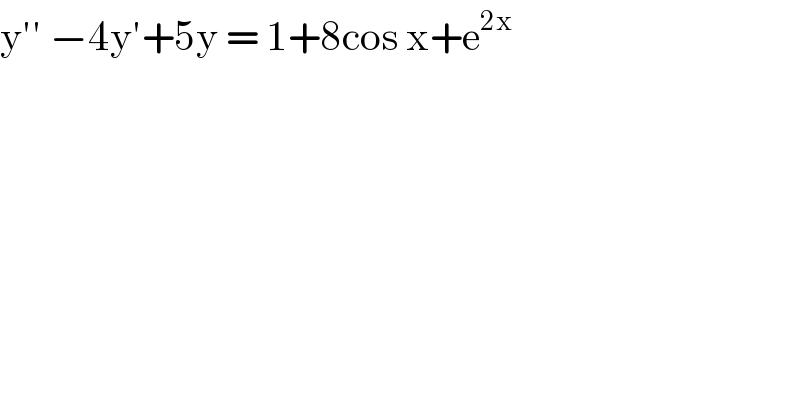
$$\mathrm{y}''\:−\mathrm{4y}'+\mathrm{5y}\:=\:\mathrm{1}+\mathrm{8cos}\:\mathrm{x}+\mathrm{e}^{\mathrm{2x}} \\ $$

Commented by niroj last updated on 11/Apr/20

(d^2 y/dx^2 )−4(dy/dx)+5y= 1+8cos x+e^(2x) (D^2 −4D+5)y= 1+8cos x +e^(2x) Auxilairy Equation, m^2 −4m+5=0 m= ((−(−4)+^− (√((−4)^2 −4.1.5)))/(2.1)) m= ((4+^− (√(16−20)))/2)= ((4+^− (√(−4)))/2) = 2+^− ((2i)/2)=2+^− 1i CF= e^(2x) (C_1 cos x+C_2 sin x) PI= ((1+8cos x+e^(2x) )/(D^2 −4D+5)) = (1/(D^2 −4D+5))+ ((8 cos x)/(D^2 −4D+5))+ (e^(2x) /(D^2 −4D+5)) = (e^(0.x) /(D^2 −4D+5)) + ((8cos x)/(−1−4D+5))+ (e^(2x) /(D^2 −4D+5)) = (e^(0.x) /((0)^2 −4.0+5)) + ((8 cos x)/(−4D+4))+ (e^(2x) /((2)^2 −4.2+5)) = (1/5)− (8/4).((cos x)/((D−1)))+ (e^(2x) /(4−8+5)) = (1/5)−((2(D+1)cos x)/((D^2 −1))) + (e^(2x) /1) = (1/5) − ((2(D+1)x cos x)/((−1−1)))+ e^(2x) = (1/5)− ((2(D+1)cos x)/(−2))+e^(2x) = (1/5)+(((D+1)cos x)/1)+e^(2x) = (1/5)+(−sin x+cos x) +e^(2x) y= CF+PI y= e^(2x) (C_1 cos x+C_2 sinx)+(1/5)−sin x+cosx +e^(2x) .

$$\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }−\mathrm{4}\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}+\mathrm{5}\boldsymbol{\mathrm{y}}=\:\mathrm{1}+\mathrm{8}\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\left(\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}\right)\mathrm{y}=\:\mathrm{1}+\mathrm{8cos}\:\mathrm{x}\:+\mathrm{e}^{\mathrm{2x}} \\ $$$$\:\:\mathrm{Auxilairy}\:\mathrm{Equation}, \\ $$$$\:\:\mathrm{m}^{\mathrm{2}} −\mathrm{4m}+\mathrm{5}=\mathrm{0} \\ $$$$\:\:\mathrm{m}=\:\frac{−\left(−\mathrm{4}\right)\overset{−} {+}\sqrt{\left(−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{1}.\mathrm{5}}}{\mathrm{2}.\mathrm{1}} \\ $$$$\:\:\:\mathrm{m}=\:\frac{\mathrm{4}\overset{−} {+}\sqrt{\mathrm{16}−\mathrm{20}}}{\mathrm{2}}=\:\frac{\mathrm{4}\overset{−} {+}\sqrt{−\mathrm{4}}}{\mathrm{2}} \\ $$$$\:\:=\:\mathrm{2}\overset{−} {+}\frac{\mathrm{2}{i}}{\mathrm{2}}=\mathrm{2}\overset{−} {+}\mathrm{1}{i} \\ $$$$\:\:\mathrm{CF}=\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\mathrm{PI}=\:\frac{\mathrm{1}+\mathrm{8cos}\:\mathrm{x}+\mathrm{e}^{\mathrm{2x}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}}+\:\frac{\mathrm{8}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}} \\ $$$$\:=\:\frac{\mathrm{e}^{\mathrm{0}.\mathrm{x}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}}\:+\:\frac{\mathrm{8cos}\:\mathrm{x}}{−\mathrm{1}−\mathrm{4D}+\mathrm{5}}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{5}} \\ $$$$=\:\:\frac{\mathrm{e}^{\mathrm{0}.\mathrm{x}} }{\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{0}+\mathrm{5}}\:+\:\frac{\mathrm{8}\:\mathrm{cos}\:\mathrm{x}}{−\mathrm{4D}+\mathrm{4}}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{2}+\mathrm{5}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}−\:\frac{\mathrm{8}}{\mathrm{4}}.\frac{\mathrm{cos}\:\mathrm{x}}{\left(\mathrm{D}−\mathrm{1}\right)}+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{4}−\mathrm{8}+\mathrm{5}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{2}\left(\mathrm{D}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{x}}{\left(\mathrm{D}^{\mathrm{2}} −\mathrm{1}\right)}\:+\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\:−\:\frac{\mathrm{2}\left(\mathrm{D}+\mathrm{1}\right)\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\left(−\mathrm{1}−\mathrm{1}\right)}+\:\mathrm{e}^{\mathrm{2x}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}−\:\frac{\mathrm{2}\left(\mathrm{D}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{x}}{−\mathrm{2}}+\mathrm{e}^{\mathrm{2x}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}+\frac{\left(\mathrm{D}+\mathrm{1}\right)\mathrm{cos}\:\mathrm{x}}{\mathrm{1}}+\mathrm{e}^{\mathrm{2x}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}+\left(−\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)\:+\mathrm{e}^{\mathrm{2x}} \\ $$$$\:\mathrm{y}=\:\mathrm{CF}+\mathrm{PI} \\ $$$$\:\:\mathrm{y}=\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sinx}\right)+\frac{\mathrm{1}}{\mathrm{5}}−\mathrm{sin}\:\mathrm{x}+\mathrm{cosx}\:+\mathrm{e}^{\mathrm{2x}} . \\ $$

Commented by jagoll last updated on 11/Apr/20