Question Number 127578 by bramlexs22 last updated on 31/Dec/20
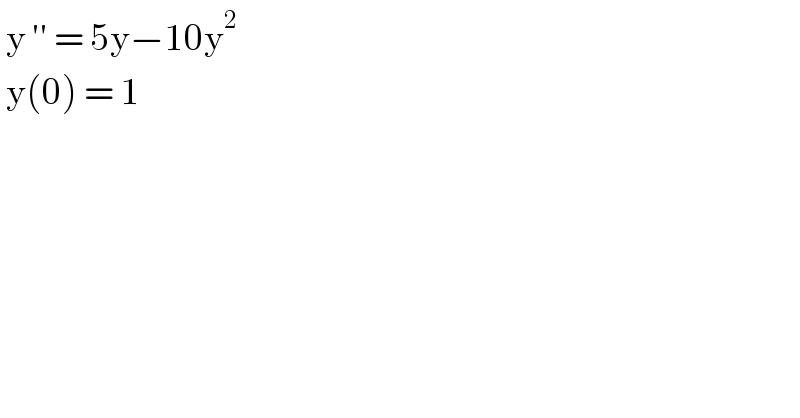
$$\:\mathrm{y}\:''\:=\:\mathrm{5y}−\mathrm{10y}^{\mathrm{2}} \\ $$$$\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$
Answered by mr W last updated on 31/Dec/20
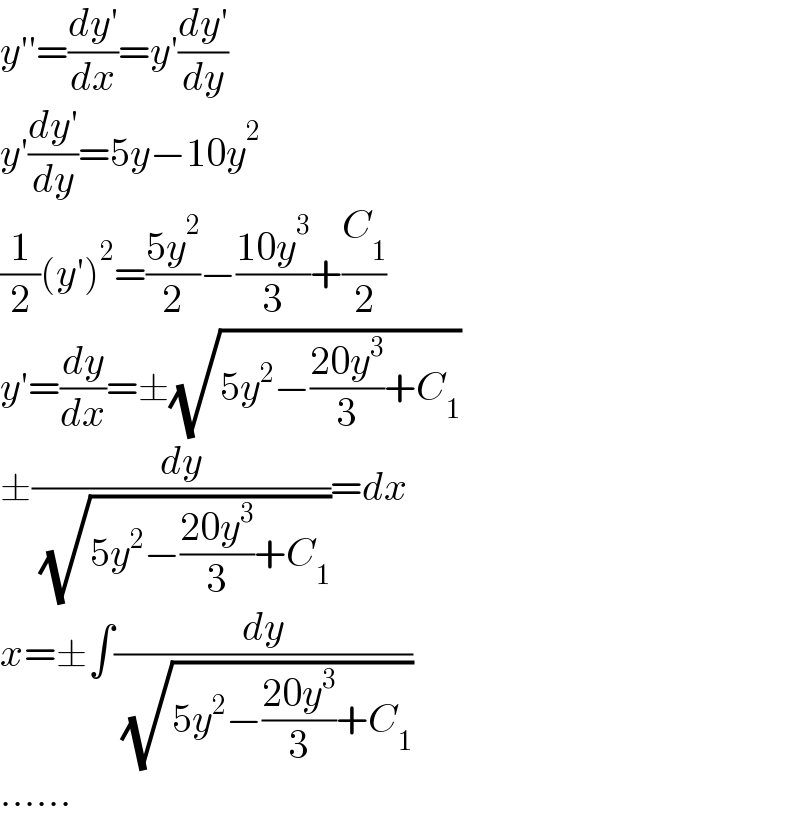
$${y}''=\frac{{dy}'}{{dx}}={y}'\frac{{dy}'}{{dy}} \\ $$$${y}'\frac{{dy}'}{{dy}}=\mathrm{5}{y}−\mathrm{10}{y}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({y}'\right)^{\mathrm{2}} =\frac{\mathrm{5}{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{10}{y}^{\mathrm{3}} }{\mathrm{3}}+\frac{{C}_{\mathrm{1}} }{\mathrm{2}} \\ $$$${y}'=\frac{{dy}}{{dx}}=\pm\sqrt{\mathrm{5}{y}^{\mathrm{2}} −\frac{\mathrm{20}{y}^{\mathrm{3}} }{\mathrm{3}}+{C}_{\mathrm{1}} } \\ $$$$\pm\frac{{dy}}{\:\sqrt{\mathrm{5}{y}^{\mathrm{2}} −\frac{\mathrm{20}{y}^{\mathrm{3}} }{\mathrm{3}}+{C}_{\mathrm{1}} }}={dx} \\ $$$${x}=\pm\int\frac{{dy}}{\:\sqrt{\mathrm{5}{y}^{\mathrm{2}} −\frac{\mathrm{20}{y}^{\mathrm{3}} }{\mathrm{3}}+{C}_{\mathrm{1}} }} \\ $$$$…… \\ $$
