Question Number 144356 by Ar Brandon last updated on 24/Jun/21

$$\mathrm{y}'+\mathrm{cos}\left(\mathrm{x}\right)\mathrm{y}=\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$
Answered by Olaf_Thorendsen last updated on 24/Jun/21
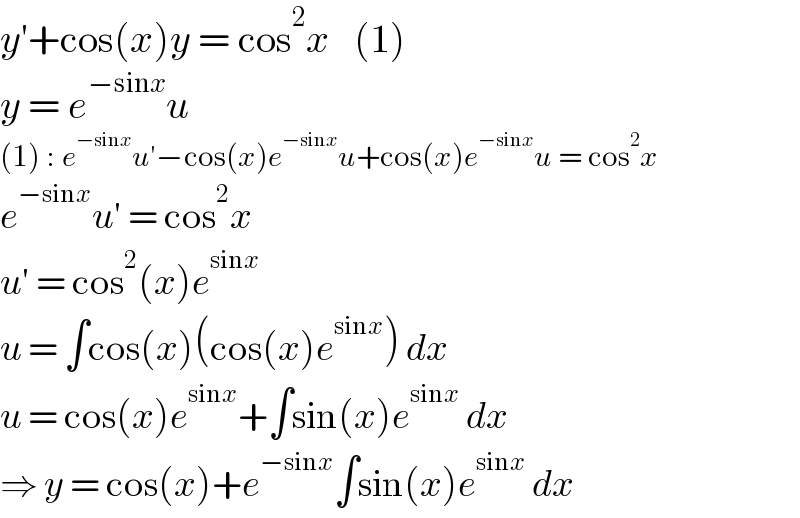
$${y}'+\mathrm{cos}\left({x}\right){y}\:=\:\mathrm{cos}^{\mathrm{2}} {x}\:\:\:\left(\mathrm{1}\right) \\ $$$${y}\:=\:{e}^{−\mathrm{sin}{x}} {u} \\ $$$$\left(\mathrm{1}\right)\::\:{e}^{−\mathrm{sin}{x}} {u}'−\mathrm{cos}\left({x}\right){e}^{−\mathrm{sin}{x}} {u}+\mathrm{cos}\left({x}\right){e}^{−\mathrm{sin}{x}} {u}\:=\:\mathrm{cos}^{\mathrm{2}} {x} \\ $$$${e}^{−\mathrm{sin}{x}} {u}'\:=\:\mathrm{cos}^{\mathrm{2}} {x} \\ $$$${u}'\:=\:\mathrm{cos}^{\mathrm{2}} \left({x}\right){e}^{\mathrm{sin}{x}} \\ $$$${u}\:=\:\int\mathrm{cos}\left({x}\right)\left(\mathrm{cos}\left({x}\right){e}^{\mathrm{sin}{x}} \right)\:{dx} \\ $$$${u}\:=\:\mathrm{cos}\left({x}\right){e}^{\mathrm{sin}{x}} +\int\mathrm{sin}\left({x}\right){e}^{\mathrm{sin}{x}} \:{dx} \\ $$$$\Rightarrow\:{y}\:=\:\mathrm{cos}\left({x}\right)+{e}^{−\mathrm{sin}{x}} \int\mathrm{sin}\left({x}\right){e}^{\mathrm{sin}{x}} \:{dx} \\ $$
