Question Number 54663 by Mikael_Marshall last updated on 08/Feb/19

$${y}\:=\:{cos}\mathrm{2}{t}×{sen}\mathrm{2}{t} \\ $$$$ \\ $$$${y}'\:=\:? \\ $$
Commented by maxmathsup by imad last updated on 08/Feb/19
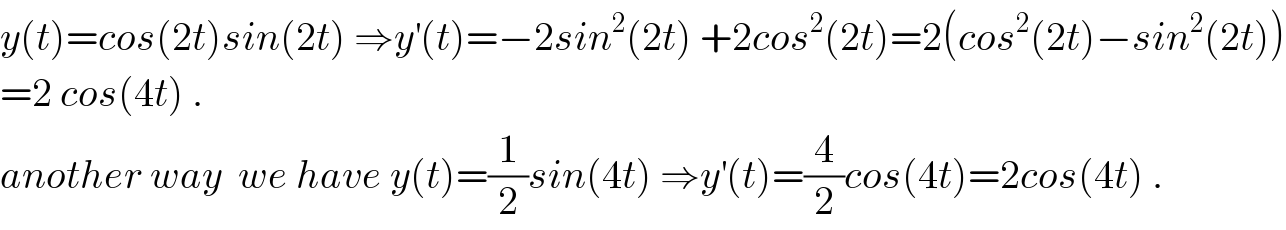
$${y}\left({t}\right)={cos}\left(\mathrm{2}{t}\right){sin}\left(\mathrm{2}{t}\right)\:\Rightarrow{y}^{'} \left({t}\right)=−\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\:+\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)=\mathrm{2}\left({cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)−{sin}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right) \\ $$$$=\mathrm{2}\:{cos}\left(\mathrm{4}{t}\right)\:. \\ $$$${another}\:{way}\:\:{we}\:{have}\:{y}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{4}{t}\right)\:\Rightarrow{y}^{'} \left({t}\right)=\frac{\mathrm{4}}{\mathrm{2}}{cos}\left(\mathrm{4}{t}\right)=\mathrm{2}{cos}\left(\mathrm{4}{t}\right)\:. \\ $$
Answered by peter frank last updated on 08/Feb/19

$${y}^{'} =\mathrm{2cos}\:\mathrm{4}{t} \\ $$
